Multippel lineær regresjon og logistisk klassifikasjon
Contents
Multippel lineær regresjon og logistisk klassifikasjon#
I dag skal vi gjøre det litt annerledes enn sist. Vi kommer til å bruke mesteparten av timen på en tutorial-oppgave som skal ta dere igjennom temaene som dere skal lære i dag. Jeg kommer til å samle opp og forklare litt underveis, men målet er at dere i hovedsak skal jobbe sammen, og at jeg skal komme rundt og veilede dere. Grunnen til det er at dette er den beste måten å lære på.
I leseleksa så dere på logistisk regresjon og på hvordan man kan validere en modell. Dette skal vi nå jobbe med.
Tutorial i logistisk regresjon#
I denne oppgaven skal vi lære å gjøre logistisk regresjon. Logistisk regresjon er en klassifiseringsmetode. Det vil si at vi ønsker å predikere kategoriske utfall. Altså utfall slik som kjønn (mann/kvinne), blodtype (A/B/AB/0) osv. Det som kjennetegner slike utfall er at de ikke enkelt kan tilordnes en numerisk verdi på en skala. Det gir ikke mening å si at blodtype B ligger midt mellom A og AB. De er bare forskjellige blodtyper. Noen ganger kan det være uklart om et utfall må være kategorisk eller om det kunne vært numerisk. Det gjelder i tilfeller der vi vet hvordan vi skal sortere kategoriene. I slike tilfeller kan det gi mening å modellere kategoriske utfall som numeriske utfall.
Hvilke av følgende utfall er kategoriske og hvilke er numeriske?
Temperatur
Navn på by
Vindstyrke
Vindretning
Politisk parti
Øltype
Karakterer
Farge
Kjønn
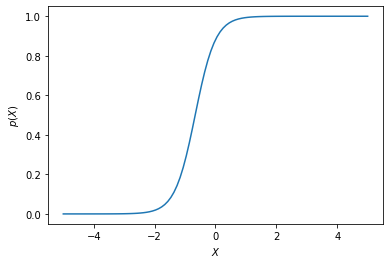
Plott den logistiske funksjonen (s. 134 i ITSL). Hvorfor er denne funksjonen egnet til å predikere et binært kategorisk utfall?
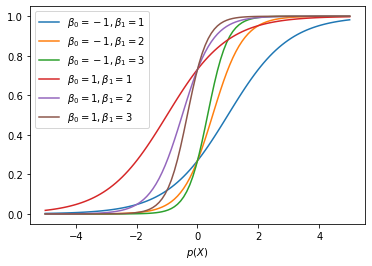
Uforsk hvordan parametrene \(\beta_0\) og \(\beta_1\) flytter på funksjonen.
Last inn
default-datasettet (https://zenodo.org/record/6199560/files/default.csv). Plott default mot hvor mye kredittkortlån en person her (balance). Ser du noen sammenheng i dataene? Lag også histogram over balansen til dem som misligholder og dem som ikke misligholder.Bruk funksjonen
np.histogramtil å lage et histogram over hvem som misligholder og ikke, og bruk deretter histogramverdiene til å regne ut relativ frekvens av mislighold som funksjon avbalance. Kodesnutten under hjelper deg på vei:
x = np.linspace(0, 3000, 100)
df_yes = data[data["default"] == 1]
hist_yes = np.histogram(df_yes["balance"], bins=x)[0]
Prøv å finne gode verdier for parametrene \(\beta_0\) og \(\beta_1\) slik at du får tegnet en logistisk funksjon som følger dataene godt.
For å slippe å implementere metoden for å gjøre logistisk regresjon på egenhånd, skal vi bruke biblioteket scikit-learn. Næremere bestemt skal vi bruke
sklearn.linear_model.LogisticRegression. Søk opp denne metoden i scikit-learn-dokumentasjonen og kjør logistisk regresjon pådefault-datasettet med barebalancesom prediktor.Lag en confusion matrix for å evaluere hvor mange ekte positive, ekte negative, falske positive og falske negative modellen produserer. Synes du modellen oppfører seg fornuftig?
Kjør nå multippel logistisk regresjon på datasettet. Hva er viktig for om noen misligholder kredittkortlånet sitt, og ved hvilke verdier av prediktorene skjer overgangen mellom mislighold og ikke mislighold? Estimer presisjonen til modellen (hvor ofte predikerer den rett og galt?)
Kjør cross-validation på den logistiske regresjonsanalysen deres. Bruk
LogisticRegressionCVfre scikit-learn. Hvordan er presisjonen til modellen når dere analyserer på denne måten? Var forskjellen fra presisjonsmålingen på treningsdata stor?
Kategoriske
Navn på by
Politisk parti (kanskje de kunne sorteres, men usannsynlig)
Øltype (med mindre man kun ser på alkohol)
Karakterer (kanskje, kanskje ikke)
Farge (kommen an på kontekst)
Kjønn
Numeriske
Temperatur
Vindstyrke
Vindretning
Karakterer (vanligvis, man regner jo gjennomsnitt)
Farge (Om man ser på bølgelengden)
Sigmoidfunksjonen slik vi bruker den i logistisk regresjon er
Denne funksjonen er godt egnet til å beregne binære utfall fordi den er begrenser på intervallet 0 til 1.
import numpy as np
import matplotlib.pyplot as plt
def logistic(beta_0, beta_1, X):
return np.exp(beta_0 + beta_1*X)/(1+np.exp(beta_0 + beta_1*X))
x = np.linspace(-5, 5, 100)
y = logistic(2, 3, x)
plt.plot(x, y)
plt.xlabel(r"$X$")
plt.ylabel(r"$p(X)$")
plt.savefig("logistic.svg")
### Auto-utforsk
beta0s = [-1, 1]
beta1s = [1, 2, 3]
for beta0 in beta0s:
for beta1 in beta1s:
x = np.linspace(-5, 5, 100)
y = logistic(beta0, beta1, x)
plt.plot(x, y, label=rf"$\beta_0 = {beta0}, \beta_1 = {beta1}$")
plt.legend()
plt.xlabel(r"$X$")
plt.xlabel(r"$p(X)$")
plt.savefig("logistic_variation.svg")
from ipywidgets import interactive
#import matplotlib.pyplot as plt
import numpy as np
def f(beta0, beta1):
x = np.linspace(-5, 5, num=1000)
plt.plot(x, logistic(beta0, beta1, x))
plt.ylim(-0.1, 1.1)
interactive_plot = interactive(f, beta0=(-3.0, 3.0), beta1=(-3, 3, 0.1))
interactive_plot
Konklusjon: \(\beta_1\) styrer hvor bratt funksjonen er og \(\beta_0\) flytter vendepunktet fram og tilbake. Men posisjonen til vendepunktet er avhengig av både \(\beta_0\) og \(\beta_1\).
import pandas as pd
df = pd.read_csv("https://zenodo.org/record/6199560/files/default.csv")
df.replace("Yes", 1, inplace=True)
df.replace("No", 0, inplace=True)
df
| Unnamed: 0 | default | student | balance | income | |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 729.526495 | 44361.625074 |
| 1 | 2 | 0 | 1 | 817.180407 | 12106.134700 |
| 2 | 3 | 0 | 0 | 1073.549164 | 31767.138947 |
| 3 | 4 | 0 | 0 | 529.250605 | 35704.493935 |
| 4 | 5 | 0 | 0 | 785.655883 | 38463.495879 |
| ... | ... | ... | ... | ... | ... |
| 9995 | 9996 | 0 | 0 | 711.555020 | 52992.378914 |
| 9996 | 9997 | 0 | 0 | 757.962918 | 19660.721768 |
| 9997 | 9998 | 0 | 0 | 845.411989 | 58636.156984 |
| 9998 | 9999 | 0 | 0 | 1569.009053 | 36669.112365 |
| 9999 | 10000 | 0 | 1 | 200.922183 | 16862.952321 |
10000 rows × 5 columns
df.plot("balance", "default", kind="scatter")
<AxesSubplot:xlabel='balance', ylabel='default'>

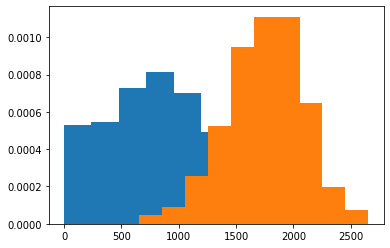
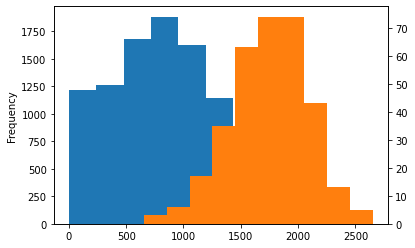
Her ser vi stort sett to klumper med data. For å klare å se litt mer av hva som skjer kan vi ta lokale gjennomsnitt for å estimere sannsynligheten for mislighold. Vi begynner med å lage histogram over parametrene default og ikke default.
# Direkte:
df_no = df[df["default"] == 0]
plt.hist(df_no["balance"], density=True)
df_yes = df[df["default"] == 1]
plt.hist(df_yes["balance"], density=True)
(array([4.50017209e-05, 9.00034419e-05, 2.55009752e-04, 5.25020078e-04,
9.45036140e-04, 1.11004245e-03, 1.11004245e-03, 6.45024667e-04,
1.95007457e-04, 7.50028682e-05]),
array([ 652.39713441, 852.5896786 , 1052.78222279, 1252.97476697,
1453.16731116, 1653.35985535, 1853.55239953, 2053.74494372,
2253.93748791, 2454.13003209, 2654.32257628]),
<BarContainer object of 10 artists>)
df.groupby("default")["balance"].plot.hist(density=False, secondary_y=[1])
default
0 AxesSubplot(0.125,0.125;0.775x0.755)
1 AxesSubplot(0.125,0.125;0.775x0.755)
Name: balance, dtype: object
# Modellere videre
import numpy as np
df.plot("balance", "default", kind="scatter")
x = np.linspace(0, 3000, 100)
df_yes = df[df["default"] == 1]
hist_yes = np.histogram(df_yes["balance"], bins=x)[0]
df_no = df[df["default"] == 0]
hist_no = np.histogram(df_no["balance"], bins=x)[0]
andel_mislighold = hist_yes/(hist_yes+hist_no)
plt.plot(x[:-1], andel_mislighold)
/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_74481/3560903358.py:13: RuntimeWarning: invalid value encountered in true_divide
andel_mislighold = hist_yes/(hist_yes+hist_no)
[<matplotlib.lines.Line2D at 0x2923c0a60>]
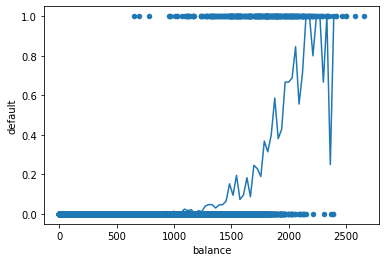
Siden vi nå har regnet ut andelen som misligholder i små intervaller av variabelen balance, har vi et estimat på sannsynlighet for mislighold gitt balance. Vi ser kanskje også at funksjonsformen ligner på den logistiske funksjonen. Derfor vil vi prøve å modellere dette datasettet med logistisk regresjon.
# Logistisk regresjon med default-datasettet
from sklearn.linear_model import LogisticRegression
X = df.loc[:, ["balance"]]
y = df.loc[:, ["default"]].to_numpy().ravel()
clf = LogisticRegression(random_state=42, C=1e-7).fit(X, y)
# Plotte modellen
import numpy as np
df.plot.scatter("balance", "default", label="data")
x = np.linspace(0, 3000, 100)
plt.plot(x[:-1], andel_mislighold, label="Binned data")
y_hat = clf.predict(x[:,np.newaxis])
plt.plot(x, y_hat, label="Prediction")
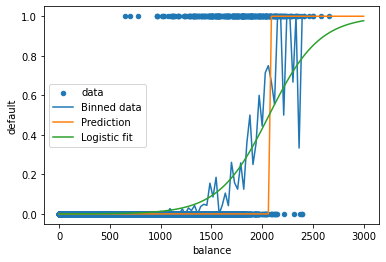
plt.plot(x, clf.predict_proba(x[:,np.newaxis])[:,1], label="Logistic fit")
plt.legend()
/Users/henriasv/.pyenv/versions/3.9.9/envs/hon2200/lib/python3.9/site-packages/sklearn/base.py:450: UserWarning: X does not have valid feature names, but LogisticRegression was fitted with feature names
warnings.warn(
/Users/henriasv/.pyenv/versions/3.9.9/envs/hon2200/lib/python3.9/site-packages/sklearn/base.py:450: UserWarning: X does not have valid feature names, but LogisticRegression was fitted with feature names
warnings.warn(
<matplotlib.legend.Legend at 0x2a5f953a0>
# Confusion matrix
from sklearn.metrics import confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay
y_hat = clf.predict(X)
print("Score: ", clf.score(X, y))
confusion_matrix(y, y_hat)
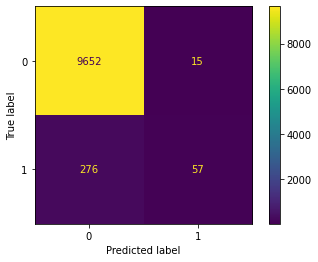
ConfusionMatrixDisplay.from_predictions(y, y_hat)
Score: 0.9709
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x2a600c340>
import matplotlib
colormap = "winter"
cmap = matplotlib.cm.get_cmap(colormap)
x = np.linspace(0, 3000, 100)
for name, value in df.groupby("student"):
df_yes = value[value["default"] == 1]
hist_yes = np.histogram(df_yes["balance"], bins=x)[0]
df_no = value[value["default"] == 0]
hist_no = np.histogram(df_no["balance"], bins=x)[0]
andel_mislighold = hist_yes/(hist_yes+hist_no)
if name == 0:
plt.plot(x[:-1], andel_mislighold, label=name, c=cmap(0.0))
elif name == 1:
plt.plot(x[:-1], andel_mislighold, label=name, c=cmap(1.0))
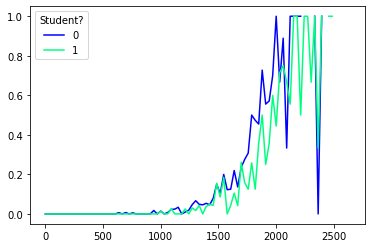
plt.legend(title="Student?")
/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_74481/3014530260.py:13: RuntimeWarning: invalid value encountered in true_divide
andel_mislighold = hist_yes/(hist_yes+hist_no)
/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_74481/3014530260.py:13: RuntimeWarning: invalid value encountered in true_divide
andel_mislighold = hist_yes/(hist_yes+hist_no)
<matplotlib.legend.Legend at 0x292c189d0>
# Logistisk regresjon med default-datasettet
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as np
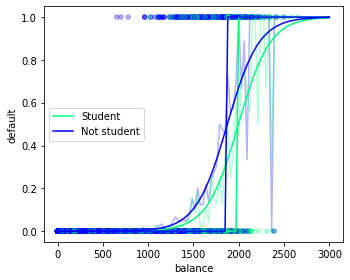
df.plot.scatter("balance", "default", c="student", cmap=colormap, alpha=0.3, sharex=False)
plt.gcf().delaxes(plt.gcf().axes[1])
x = np.linspace(0, 3000, 100)
for is_student, subset in df.groupby("student"):
df_yes = subset[subset["default"] == 1]
hist_yes = np.histogram(df_yes["balance"], bins=x)[0]
df_no = subset[subset["default"] == 0]
hist_no = np.histogram(df_no["balance"], bins=x)[0]
andel_mislighold = hist_yes/(hist_yes+hist_no)
if is_student == 0:
plt.plot(x[:-1], andel_mislighold, c=cmap(0.0), alpha=0.3)
elif is_student == 1:
plt.plot(x[:-1], andel_mislighold, c=cmap(1.0), alpha=0.3)
X = df.loc[:, ["balance", "student"]]
y = df.loc[:, ["default"]].to_numpy().ravel()
clf = LogisticRegression(random_state=42).fit(X, y)
x = pd.DataFrame({"balance" : np.linspace(0, 3000, 100), "student" : np.ones(100)})
plt.plot(x["balance"], clf.predict_proba(x)[:,1], label="Student", c=cmap(1.0))
plt.plot(x["balance"], clf.predict(x), c=cmap(1.0))
x = pd.DataFrame({"balance" : np.linspace(0, 3000, 100), "student" : np.zeros(100)})
plt.plot(x["balance"], clf.predict_proba(x)[:,1], label="Not student", c=cmap(0.0))
plt.plot(x["balance"], clf.predict(x), c=cmap(0.0))
plt.legend()
plt.tight_layout()
/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_74481/2483415999.py:17: RuntimeWarning: invalid value encountered in true_divide
andel_mislighold = hist_yes/(hist_yes+hist_no)
/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_74481/2483415999.py:17: RuntimeWarning: invalid value encountered in true_divide
andel_mislighold = hist_yes/(hist_yes+hist_no)
# Confusion matrix
from sklearn.metrics import confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay
X = df.loc[:, ["balance", "student"]]
y = df.loc[:, ["default"]].to_numpy().ravel()
clf = LogisticRegression(random_state=42, C=1e4).fit(X, y)
print("Score: ", clf.score(X, y))
y_hat = clf.predict(X)
print(confusion_matrix(y, y_hat))
ConfusionMatrixDisplay.from_predictions(y, y_hat)
Score: 0.9733
[[9628 39]
[ 228 105]]
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x2a613c220>
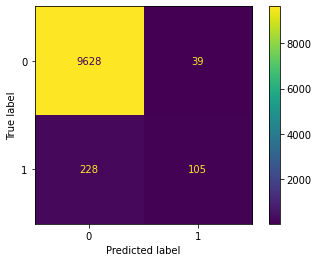
Dette er egentlig ganske bedrøvelig. Vi klarer bare å fange opp en tredel av dem som misligholder kredittkortlånet sitt. Men det kan allikevel være nyttig, for det bør kutte utlånstapene på nye lån med minimum en tredel. Og vi finner flere misligholdere enn vi mister gode betalere.
# Confusion matrix
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay
X = df.loc[:, ["balance", "student"]]
y = df.loc[:, ["default"]].to_numpy().ravel()
clf = LogisticRegressionCV(random_state=3, cv=10, tol=1e-7, Cs = [1e4]).fit(X, y)
print("Score: ", clf.scores_)
print("Coef: ", clf.coef_)
y_hat = clf.predict(X)
print(confusion_matrix(y, y_hat))
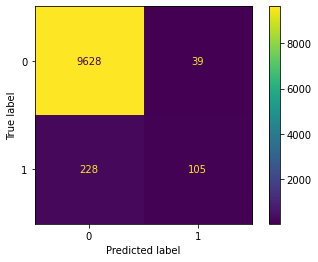
ConfusionMatrixDisplay.from_predictions(y, y_hat)
Score: {1: array([[0.972],
[0.979],
[0.971],
[0.977],
[0.971],
[0.971],
[0.971],
[0.974],
[0.978],
[0.969]])}
Coef: [[ 0.00573987 -0.71556183]]
[[9628 39]
[ 228 105]]
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x2a585da30>
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
import pandas as pd
X,y = load_iris(as_frame=True, return_X_y=True)
X["target"] = y
clf = LogisticRegression(random_state=42).fit(X, y)
#print(clf.predict(X[:2, :]))
#print(clf.predict_proba(X[:2, :]))
clf.score(X, y)
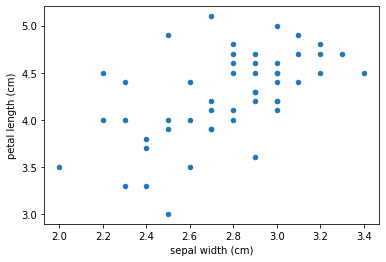
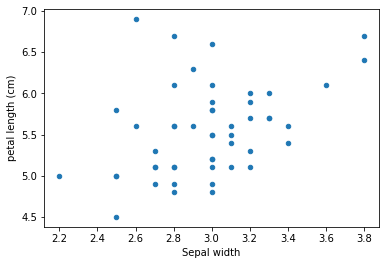
ax = plt.subplot()
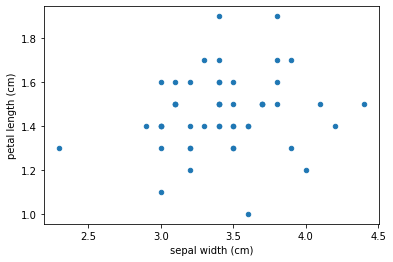
for name, subframe in X.groupby("target"):
subframe.plot(1, 2, kind="scatter", ax=ax, )
#plt.plot(X[:,0], X[:,1], )
plt.xlabel("Sepal length")
plt.xlabel("Sepal width")
display(data)
display(target)
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
5 5.4 3.9 1.7 0.4
6 4.6 3.4 1.4 0.3
7 5.0 3.4 1.5 0.2
8 4.4 2.9 1.4 0.2
9 4.9 3.1 1.5 0.1
10 5.4 3.7 1.5 0.2
11 4.8 3.4 1.6 0.2
12 4.8 3.0 1.4 0.1
13 4.3 3.0 1.1 0.1
14 5.8 4.0 1.2 0.2
15 5.7 4.4 1.5 0.4
16 5.4 3.9 1.3 0.4
17 5.1 3.5 1.4 0.3
18 5.7 3.8 1.7 0.3
19 5.1 3.8 1.5 0.3
20 5.4 3.4 1.7 0.2
21 5.1 3.7 1.5 0.4
22 4.6 3.6 1.0 0.2
23 5.1 3.3 1.7 0.5
24 4.8 3.4 1.9 0.2
25 5.0 3.0 1.6 0.2
26 5.0 3.4 1.6 0.4
27 5.2 3.5 1.5 0.2
28 5.2 3.4 1.4 0.2
29 4.7 3.2 1.6 0.2
30 4.8 3.1 1.6 0.2
31 5.4 3.4 1.5 0.4
32 5.2 4.1 1.5 0.1
33 5.5 4.2 1.4 0.2
34 4.9 3.1 1.5 0.2
35 5.0 3.2 1.2 0.2
36 5.5 3.5 1.3 0.2
37 4.9 3.6 1.4 0.1
38 4.4 3.0 1.3 0.2
39 5.1 3.4 1.5 0.2
40 5.0 3.5 1.3 0.3
41 4.5 2.3 1.3 0.3
42 4.4 3.2 1.3 0.2
43 5.0 3.5 1.6 0.6
44 5.1 3.8 1.9 0.4
45 4.8 3.0 1.4 0.3
46 5.1 3.8 1.6 0.2
47 4.6 3.2 1.4 0.2
48 5.3 3.7 1.5 0.2
49 5.0 3.3 1.4 0.2
target
0 0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
10 0
11 0
12 0
13 0
14 0
15 0
16 0
17 0
18 0
19 0
20 0
21 0
22 0
23 0
24 0
25 0
26 0
27 0
28 0
29 0
30 0
31 0
32 0
33 0
34 0
35 0
36 0
37 0
38 0
39 0
40 0
41 0
42 0
43 0
44 0
45 0
46 0
47 0
48 0
49 0
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
50 7.0 3.2 4.7 1.4
51 6.4 3.2 4.5 1.5
52 6.9 3.1 4.9 1.5
53 5.5 2.3 4.0 1.3
54 6.5 2.8 4.6 1.5
55 5.7 2.8 4.5 1.3
56 6.3 3.3 4.7 1.6
57 4.9 2.4 3.3 1.0
58 6.6 2.9 4.6 1.3
59 5.2 2.7 3.9 1.4
60 5.0 2.0 3.5 1.0
61 5.9 3.0 4.2 1.5
62 6.0 2.2 4.0 1.0
63 6.1 2.9 4.7 1.4
64 5.6 2.9 3.6 1.3
65 6.7 3.1 4.4 1.4
66 5.6 3.0 4.5 1.5
67 5.8 2.7 4.1 1.0
68 6.2 2.2 4.5 1.5
69 5.6 2.5 3.9 1.1
70 5.9 3.2 4.8 1.8
71 6.1 2.8 4.0 1.3
72 6.3 2.5 4.9 1.5
73 6.1 2.8 4.7 1.2
74 6.4 2.9 4.3 1.3
75 6.6 3.0 4.4 1.4
76 6.8 2.8 4.8 1.4
77 6.7 3.0 5.0 1.7
78 6.0 2.9 4.5 1.5
79 5.7 2.6 3.5 1.0
80 5.5 2.4 3.8 1.1
81 5.5 2.4 3.7 1.0
82 5.8 2.7 3.9 1.2
83 6.0 2.7 5.1 1.6
84 5.4 3.0 4.5 1.5
85 6.0 3.4 4.5 1.6
86 6.7 3.1 4.7 1.5
87 6.3 2.3 4.4 1.3
88 5.6 3.0 4.1 1.3
89 5.5 2.5 4.0 1.3
90 5.5 2.6 4.4 1.2
91 6.1 3.0 4.6 1.4
92 5.8 2.6 4.0 1.2
93 5.0 2.3 3.3 1.0
94 5.6 2.7 4.2 1.3
95 5.7 3.0 4.2 1.2
96 5.7 2.9 4.2 1.3
97 6.2 2.9 4.3 1.3
98 5.1 2.5 3.0 1.1
99 5.7 2.8 4.1 1.3
target
50 1
51 1
52 1
53 1
54 1
55 1
56 1
57 1
58 1
59 1
60 1
61 1
62 1
63 1
64 1
65 1
66 1
67 1
68 1
69 1
70 1
71 1
72 1
73 1
74 1
75 1
76 1
77 1
78 1
79 1
80 1
81 1
82 1
83 1
84 1
85 1
86 1
87 1
88 1
89 1
90 1
91 1
92 1
93 1
94 1
95 1
96 1
97 1
98 1
99 1
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) \
100 6.3 3.3 6.0 2.5
101 5.8 2.7 5.1 1.9
102 7.1 3.0 5.9 2.1
103 6.3 2.9 5.6 1.8
104 6.5 3.0 5.8 2.2
105 7.6 3.0 6.6 2.1
106 4.9 2.5 4.5 1.7
107 7.3 2.9 6.3 1.8
108 6.7 2.5 5.8 1.8
109 7.2 3.6 6.1 2.5
110 6.5 3.2 5.1 2.0
111 6.4 2.7 5.3 1.9
112 6.8 3.0 5.5 2.1
113 5.7 2.5 5.0 2.0
114 5.8 2.8 5.1 2.4
115 6.4 3.2 5.3 2.3
116 6.5 3.0 5.5 1.8
117 7.7 3.8 6.7 2.2
118 7.7 2.6 6.9 2.3
119 6.0 2.2 5.0 1.5
120 6.9 3.2 5.7 2.3
121 5.6 2.8 4.9 2.0
122 7.7 2.8 6.7 2.0
123 6.3 2.7 4.9 1.8
124 6.7 3.3 5.7 2.1
125 7.2 3.2 6.0 1.8
126 6.2 2.8 4.8 1.8
127 6.1 3.0 4.9 1.8
128 6.4 2.8 5.6 2.1
129 7.2 3.0 5.8 1.6
130 7.4 2.8 6.1 1.9
131 7.9 3.8 6.4 2.0
132 6.4 2.8 5.6 2.2
133 6.3 2.8 5.1 1.5
134 6.1 2.6 5.6 1.4
135 7.7 3.0 6.1 2.3
136 6.3 3.4 5.6 2.4
137 6.4 3.1 5.5 1.8
138 6.0 3.0 4.8 1.8
139 6.9 3.1 5.4 2.1
140 6.7 3.1 5.6 2.4
141 6.9 3.1 5.1 2.3
142 5.8 2.7 5.1 1.9
143 6.8 3.2 5.9 2.3
144 6.7 3.3 5.7 2.5
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
target
100 2
101 2
102 2
103 2
104 2
105 2
106 2
107 2
108 2
109 2
110 2
111 2
112 2
113 2
114 2
115 2
116 2
117 2
118 2
119 2
120 2
121 2
122 2
123 2
124 2
125 2
126 2
127 2
128 2
129 2
130 2
131 2
132 2
133 2
134 2
135 2
136 2
137 2
138 2
139 2
140 2
141 2
142 2
143 2
144 2
145 2
146 2
147 2
148 2
149 2
/Users/henriasv/.pyenv/versions/3.9.9/envs/hon2200/lib/python3.9/site-packages/sklearn/linear_model/_logistic.py:814: ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
Increase the number of iterations (max_iter) or scale the data as shown in:
https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
n_iter_i = _check_optimize_result(
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
/Users/henriasv/repos/data-drevne-prosjekter-hon2200/data_drevne_prosjekter/ferdighetstrening/notebooks/03_forelesning_multippel_og_logistisk.ipynb Cell 20' in <module>
<a href='vscode-notebook-cell:/Users/henriasv/repos/data-drevne-prosjekter-hon2200/data_drevne_prosjekter/ferdighetstrening/notebooks/03_forelesning_multippel_og_logistisk.ipynb#ch0000005?line=16'>17</a> plt.xlabel("Sepal length")
<a href='vscode-notebook-cell:/Users/henriasv/repos/data-drevne-prosjekter-hon2200/data_drevne_prosjekter/ferdighetstrening/notebooks/03_forelesning_multippel_og_logistisk.ipynb#ch0000005?line=17'>18</a> plt.xlabel("Sepal width")
---> <a href='vscode-notebook-cell:/Users/henriasv/repos/data-drevne-prosjekter-hon2200/data_drevne_prosjekter/ferdighetstrening/notebooks/03_forelesning_multippel_og_logistisk.ipynb#ch0000005?line=19'>20</a> display(data)
<a href='vscode-notebook-cell:/Users/henriasv/repos/data-drevne-prosjekter-hon2200/data_drevne_prosjekter/ferdighetstrening/notebooks/03_forelesning_multippel_og_logistisk.ipynb#ch0000005?line=20'>21</a> display(target)
NameError: name 'data' is not defined
<Figure size 432x288 with 0 Axes>
Beslutningstrær#
Dette er noe vi har med fordi det danner grunnlaget for en veldig kraftig metode som heter XGBoost. Vi krever ikke at dere forstår metoden fullt ut, men ønsker at dere skal ha en viss forståelse for hvordan det fungerer. Vi kommer til å legge mest vekt på at dere kan gjøre fornuftig feilanalyse av modellene, slik at metoden i seg selv i stor grad kan behandles som en svart boks.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
df = pd.read_csv("https://zenodo.org/record/6075333/files/Boston.csv")
df = df.sort_values(by="nox")
X = df[["nox", "lstat"]].values # Pass på antall klammer
Y = df[["medv"]].values
linear_model = LinearRegression().fit(X, Y)
print(linear_model.coef_)
print(linear_model.intercept_)
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:,0], X[:,1], Y, marker='.', color='red')
y_pred = linear_model.predict(X)
coefs = linear_model.coef_
intercept = linear_model.intercept_
xs = np.tile(np.linspace(0.4, 0.9, 10), (10,1))
ys = np.tile(np.linspace(0, 40, 10), (10,1)).T
zs = xs*coefs[0,0]+ys*coefs[0,1]+intercept
ax.plot_surface(xs,ys,zs, alpha=0.5)
ax.set_xlabel("nox")
ax.set_ylabel("lstat")
ax.view_init(elev=90., azim=180)
[[ 1.04245301 -0.96004457]]
[34.10206739]
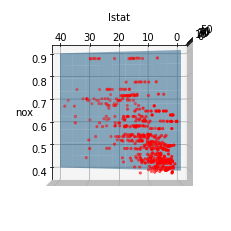
Ved å variere synsvinkelen kan vi finne at nox-nivået varierer med andelen lavere status innbyggere, og at denne egenskapen har tatt over som det den lineære modellen plukker opp. Men det er jo fortsatt et spørsmål om hva som er høna og egget.
