Forelesningsnotat: Lineær regresjon og modellering

Henrik Sveinsson

Slide-versjon

Forrige uke

• Datasett
  • Numpy
  • Pandas
  • Sette opp manuel/lese inn fra fil
• Plotting

I dag

Hvordan kan vi lære noe av et datasett?

• Lineær regresjon
• Estimere feilen i estimerte parametre

Husk

Ikke alt dekkes i forelesninger. Noe er bare i boka

Forrige ukes oppgaver

• Når ble varmepumpen installert?
• Og viktigst: Hvordan fant dere ut av det? Det krever litt kreativitet.

En skisse av en løsning

La oss anta at vi har lest inn prisdata fra nordpool og lagt dem i en csv-fil. Så begynner vi med prisen på strømmen.

import pandas as pd
df_pris = pd.read_csv("data/nordpool-dec-24.csv")
df_forbruk = pd.read_csv("data/meteringvalues-dec-2024.csv", sep=";", decimal=",")

nettopris = sum(df_forbruk['KWH 60 Forbruk']*df_pris["value"])/1000
med_moms = nettopris*1.25
print(f"Spotpris på strømmen inkl. moms er {med_moms:.2f} kr")

Spotpris på strømmen inkl. moms er 2899.55 kr

Hva med varmepumpa?

Først må vi ha værdata. Jeg antar vi har lagret det i en fil weather_blindern.json.

import json 
with open("data/weather_blindern.json") as ifile:
    json_content = json.load(ifile)
my_list = []
for data in json_content["data"]:
    my_list += data["observations"]
df_temp = pd.DataFrame(my_list)
df_temp = df_temp[df_temp["timeOffset"] == "PT6H"]
print(df_temp.head())

                   elementId  value  unit  \
1  mean(air_temperature P1D)    7.2  degC   
3  mean(air_temperature P1D)    7.8  degC   
5  mean(air_temperature P1D)    4.2  degC   
7  mean(air_temperature P1D)   -3.5  degC   
9  mean(air_temperature P1D)   -3.5  degC   

                                               level timeOffset  \
1  {'levelType': 'height_above_ground', 'unit': '...       PT6H   
3  {'levelType': 'height_above_ground', 'unit': '...       PT6H   
5  {'levelType': 'height_above_ground', 'unit': '...       PT6H   
7  {'levelType': 'height_above_ground', 'unit': '...       PT6H   
9  {'levelType': 'height_above_ground', 'unit': '...       PT6H   

  timeResolution  timeSeriesId performanceCategory exposureCategory  \
1            P1D             0                   C                2   
3            P1D             0                   C                2   
5            P1D             0                   C                2   
7            P1D             0                   C                2   
9            P1D             0                   C                2   

   qualityCode  
1          NaN  
3          NaN  
5          NaN  
7          NaN  
9          NaN  

Kjøre sammen dataene

from datetime import datetime
def date_func(row): 
    date_object = datetime.strptime(row["Fra"], "%d.%m.%Y %H:%M")
    return date_object.date()

df_forbruk["date"] = df_forbruk.apply(date_func, axis=1) 
forbruk_per_dag = df_forbruk.groupby("date").sum()
x = df_temp["value"]
y = forbruk_per_dag["KWH 60 Forbruk"]

Plotte

Text(0, 0.5, 'Strømforbruk [kWh]')

Hva nå?

Så stirrer vi på grafene og ser etter om det er noe valg som gir oss to klare grupper med datapunkter.

Leseleksen

• Skriv opp tre konsepter du forstod, og tre konsepter du ikke forstod

Oppgave

• Skriv opp på tre forskjellige postit-lapper, konseptene du ikke forstod. Alle legger lappene sammen i en bunke. SÅ tar dere dem en og en og ser om dere kan få forklart dem på gruppa
• Etterpå oppsummerer vi litt i plenum

Ohms lov og lineær regresjon

Fra strøm i naturfag på vgs/ungdomsskolen vet vi at \[U = RI \implies I = \frac{1}{R}U\]

Kan plotte:

Strøm \(I\) er en lineær funksjon av spenning \(U\), med invers motstand som proporsjonalitetskonstant.

Måledata

Vi går på laben og finner en Ohmsk motstand, og måler, da forventer vi å finne noe slikt:

Finne stigningstallet

Siden stigningen er 3.33…, så er motstanden \(0.3 \Omega\).

Dermed kan vi plotte en linje sammen med datapunktene

Men er det slik måleserier ser ut i virkeligheten?

Støy

Vi får nok heller noe som ser slik ut:

Er dette en god ide?

Lineær regresjon

Nå må vi forholde oss til verden slik den er. Det er alltid en viss usikkerhet vi ikke klarer å forklare uansett hvor god modell vi har. \[y=f(x) + \varepsilon\]

Der \(\varepsilon\) representeter en usikkerhet som vi ikke klarer å plukke opp med vår modell av fenomenet.

Lineær regresjon

Vi ønsker å finne parametre \(\beta_0\) og \(\beta_1\) i funksjonen \[f(x) = \beta_1 x + \beta_0\]

Slik at når vi sier at \(\hat{y} = f(x)\), så minimerer vi

\[\sum_{i=0}^N (y_i - \hat{y}_i)^2\]

Dette heter minste kvadraters lineær regresjon.

Lineær regresjon med numpy

import numpy as np
p = np.polyfit(U, I, 1)
print(p)

[3.34088808 0.17706321]

Plotte sammen

Oppgave

Skriv opp for deg selv, hva som er sammenhengen mellom den rette linja og datapunktene her om vi har gjort lineær regresjon.

Prøve flere ganger

Trekke mange ganger

Oppgave

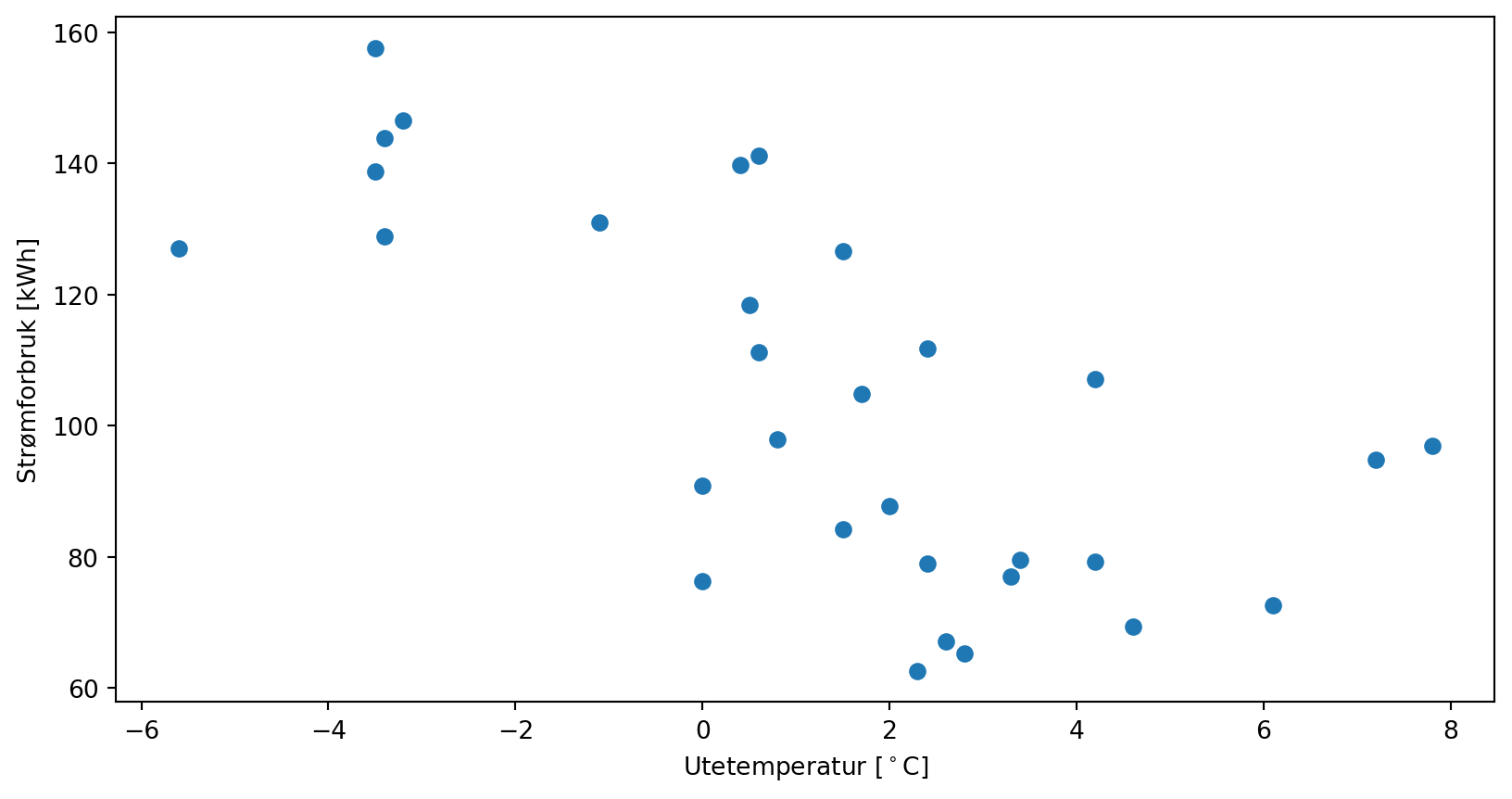
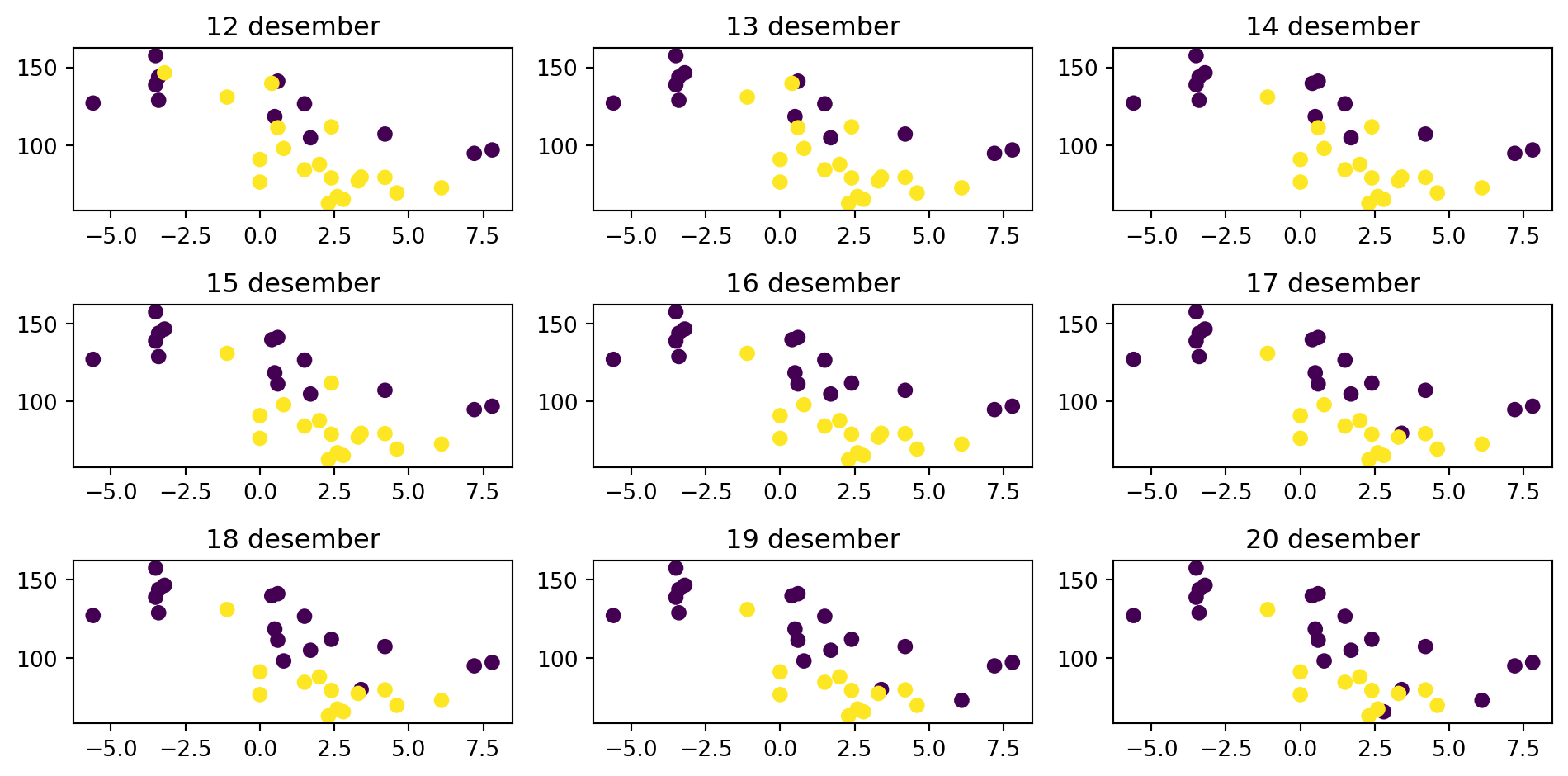
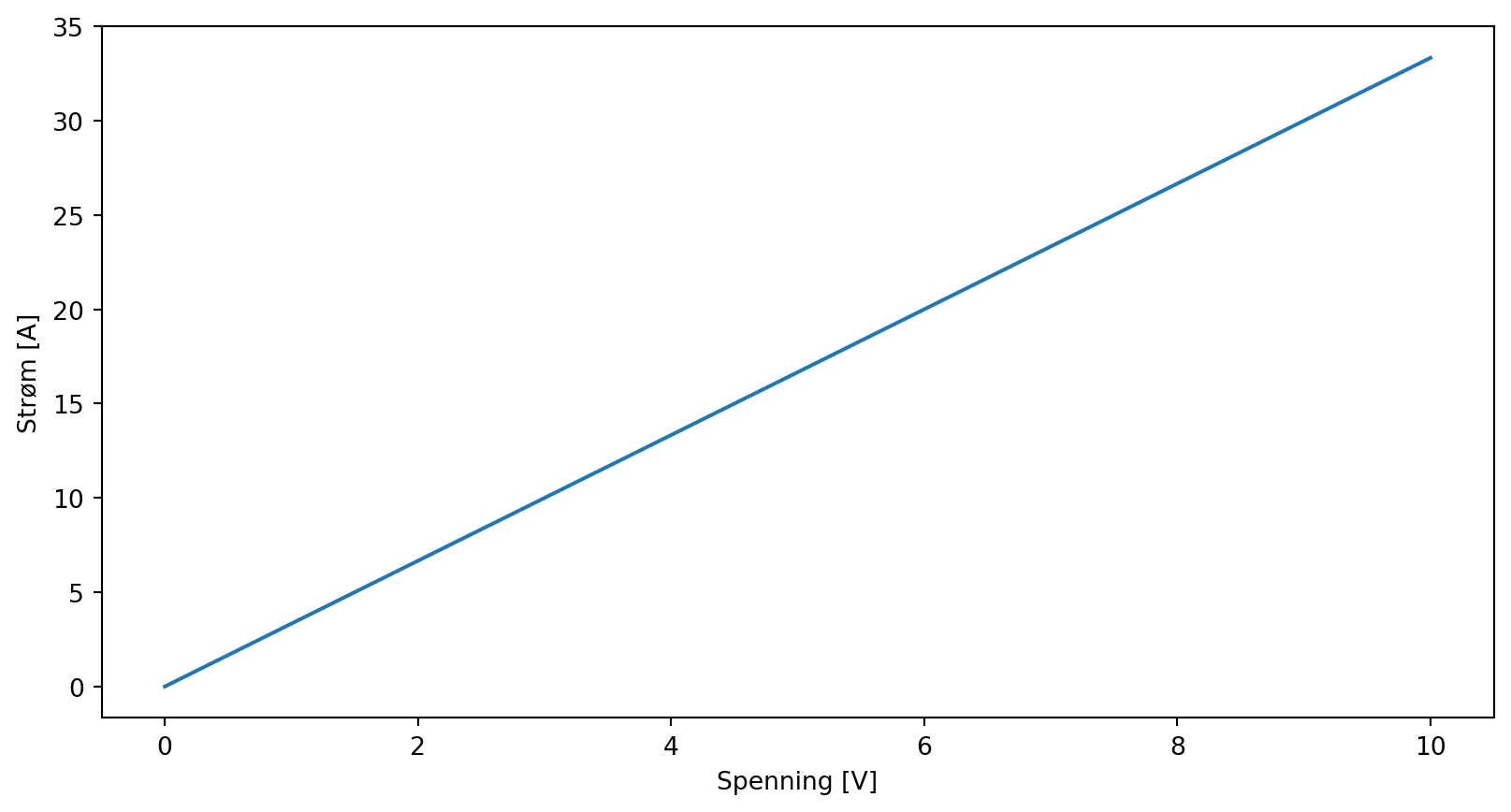
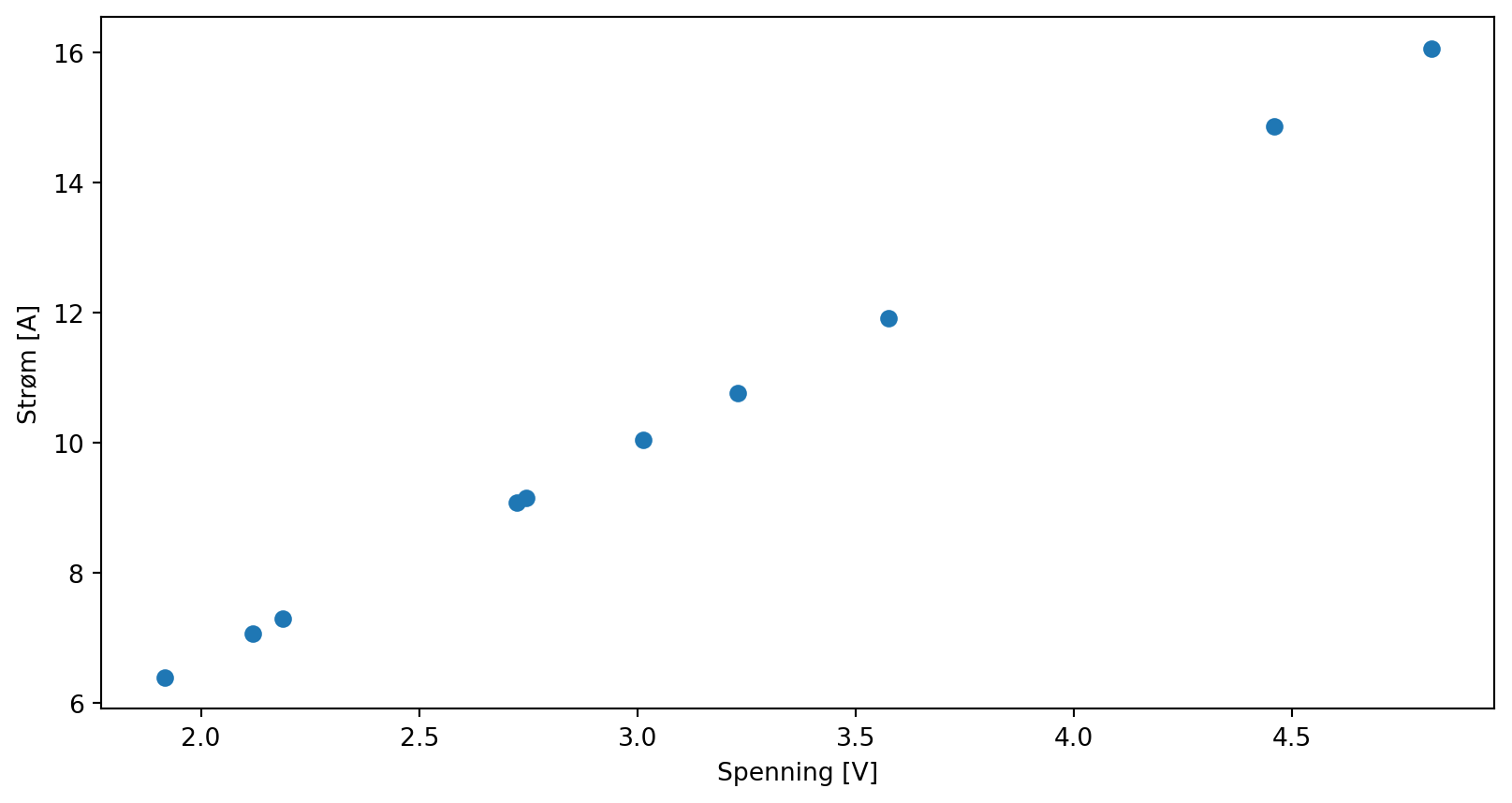
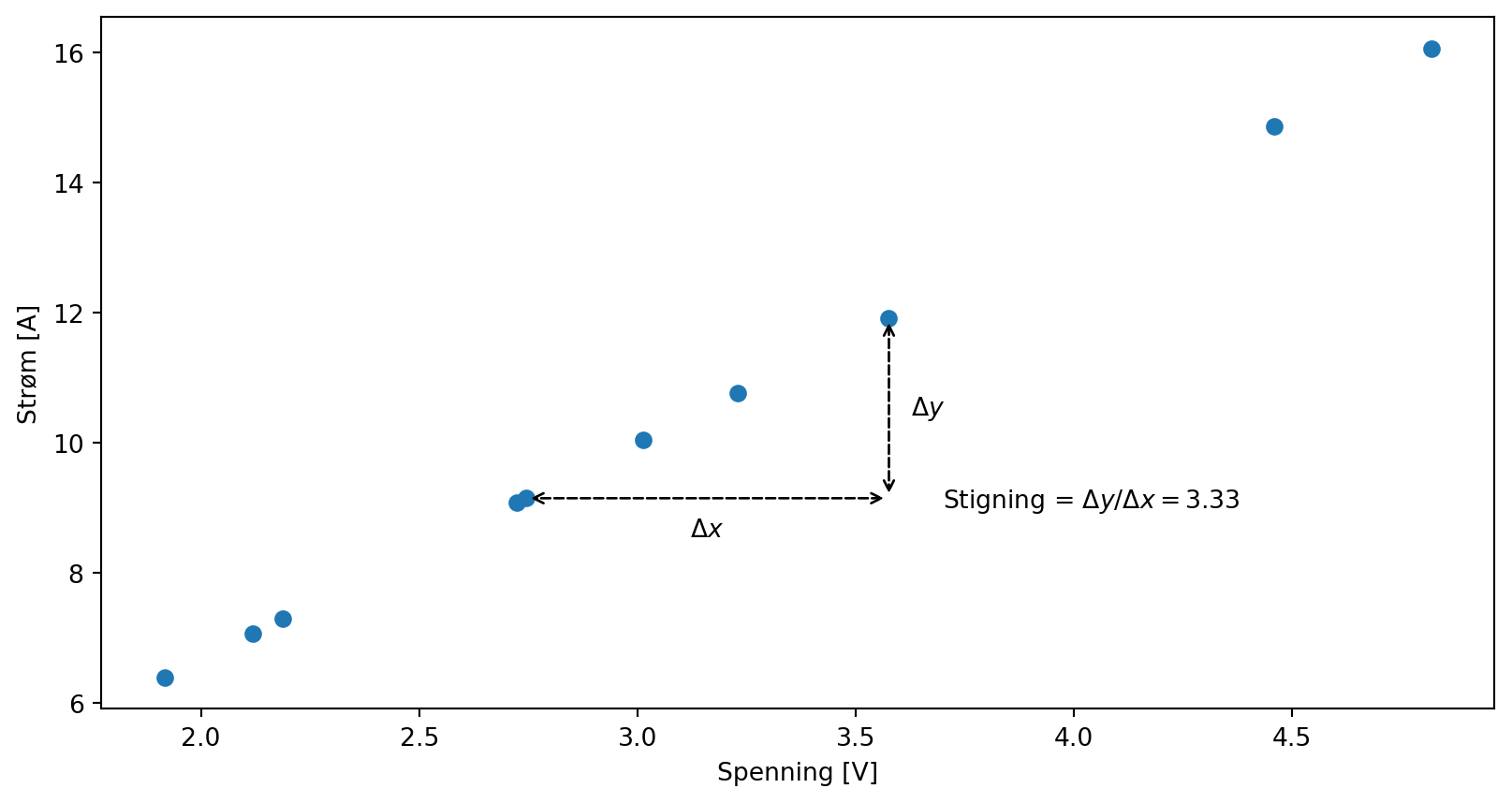
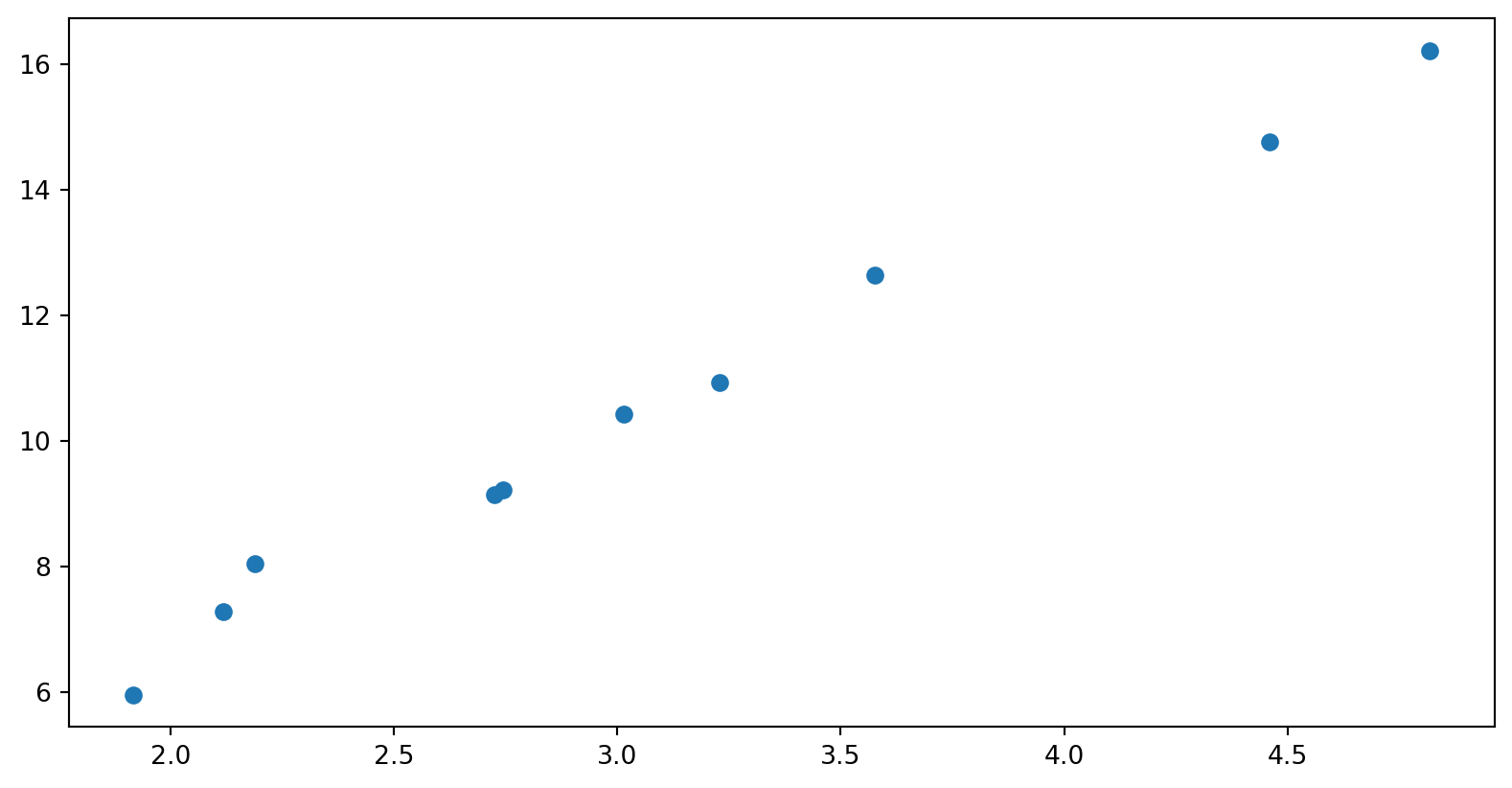
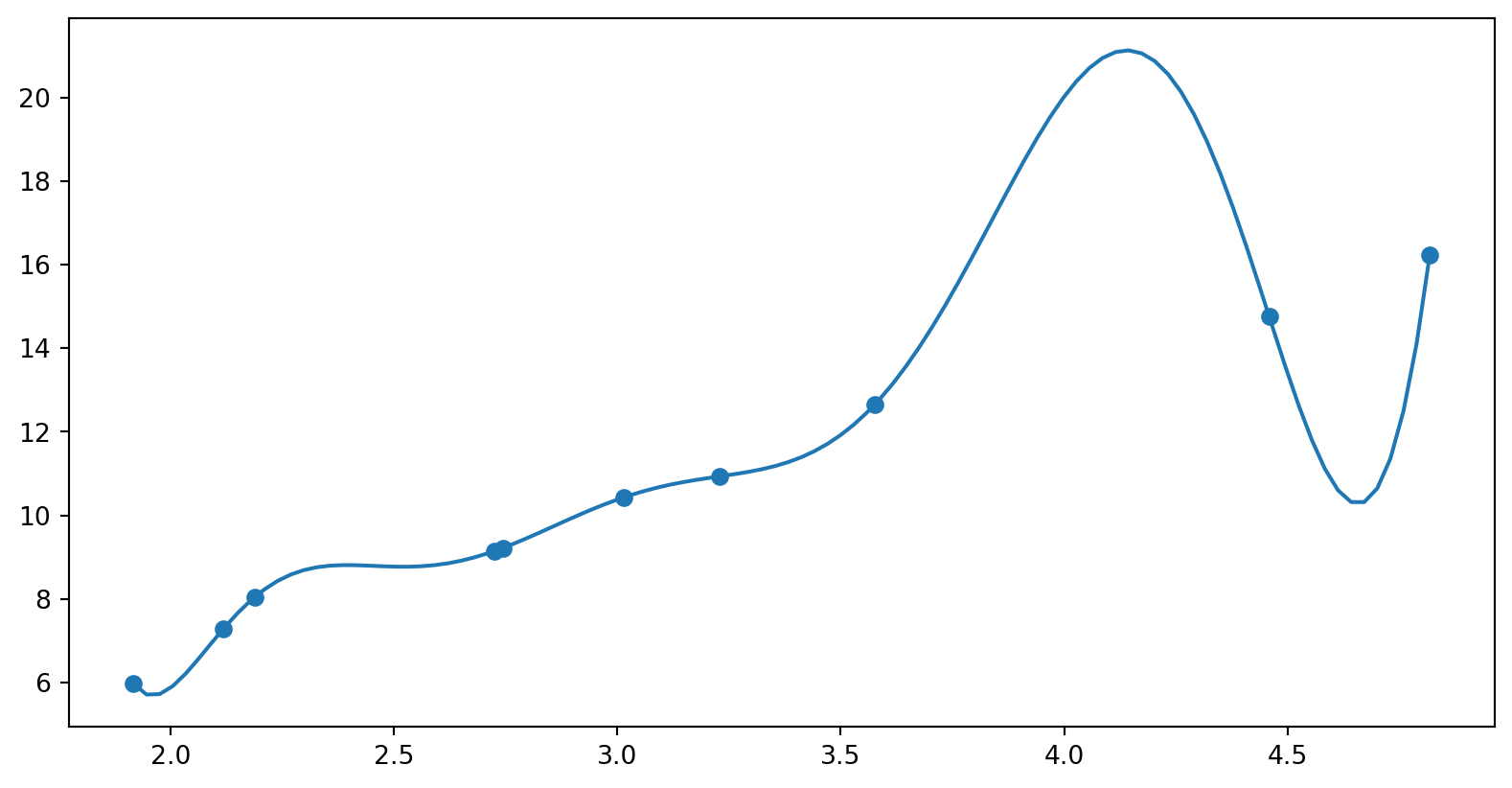
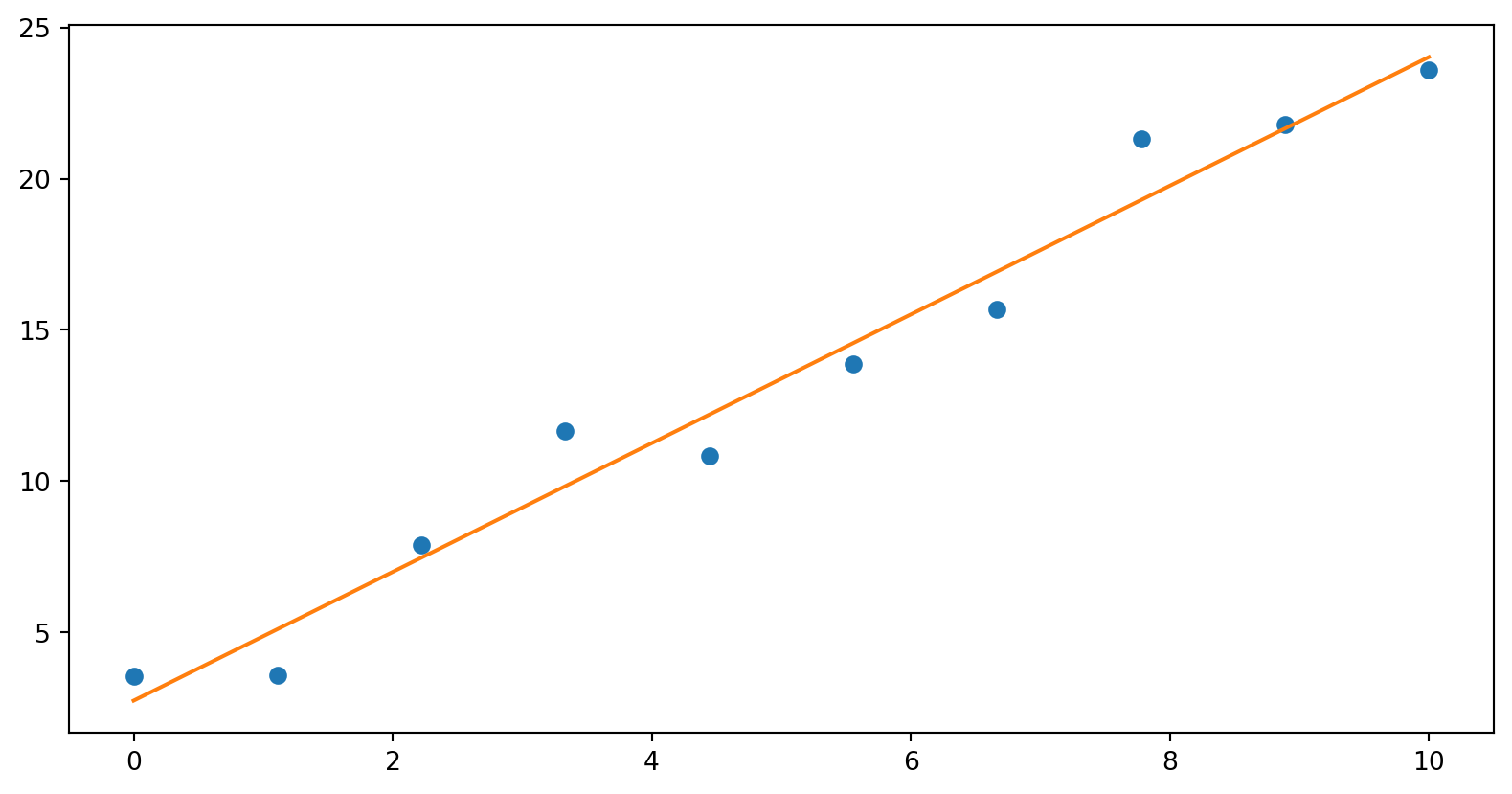
a) Lag deg en affin funsjon (f. eks \(f(x) = 2x + 3\)). Trekk 10 tilfeldige tall, beregn \(f(x) + \varepsilon\) der du setter inn et tilfeldig normalfordelt tall som \(\varepsilon\) med np.random.normal(...). Verifiser med et plott at ting fungerer som de skal

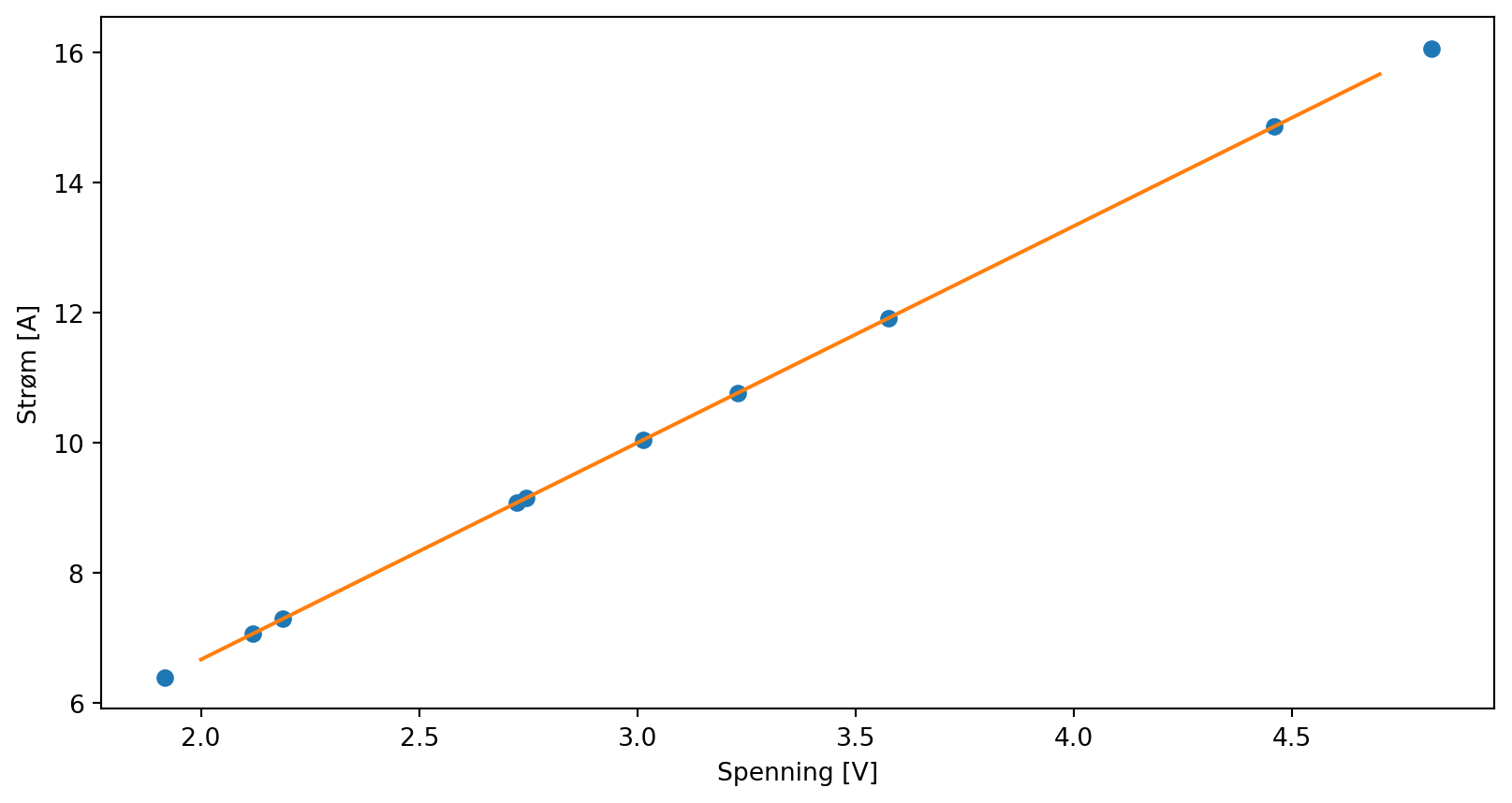
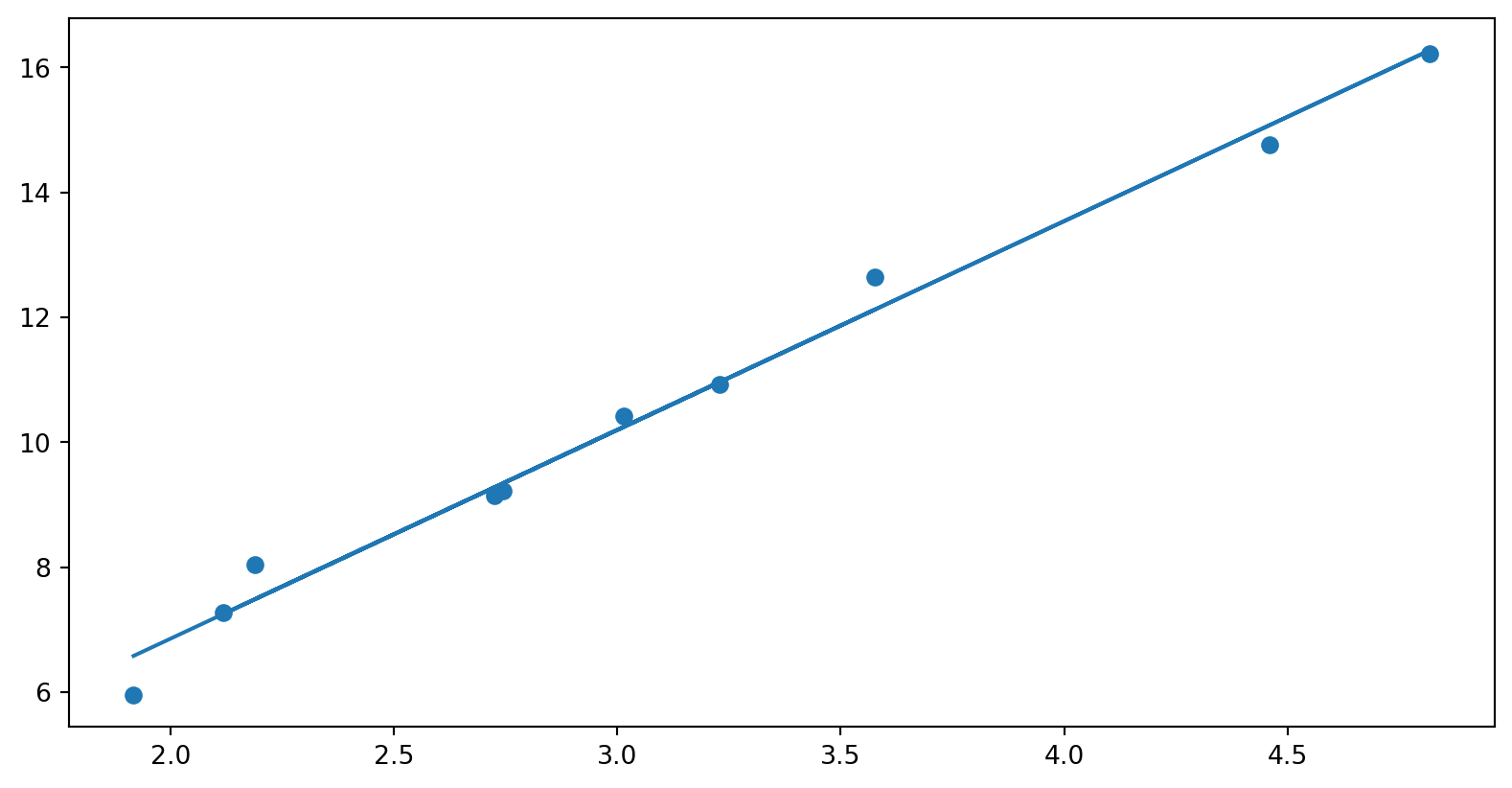
b) Gjør en lineærtilpasning med np.polyfit(x, y, 1). Plott lineærtilpasningen sammen med de litt spredte punktene dine.

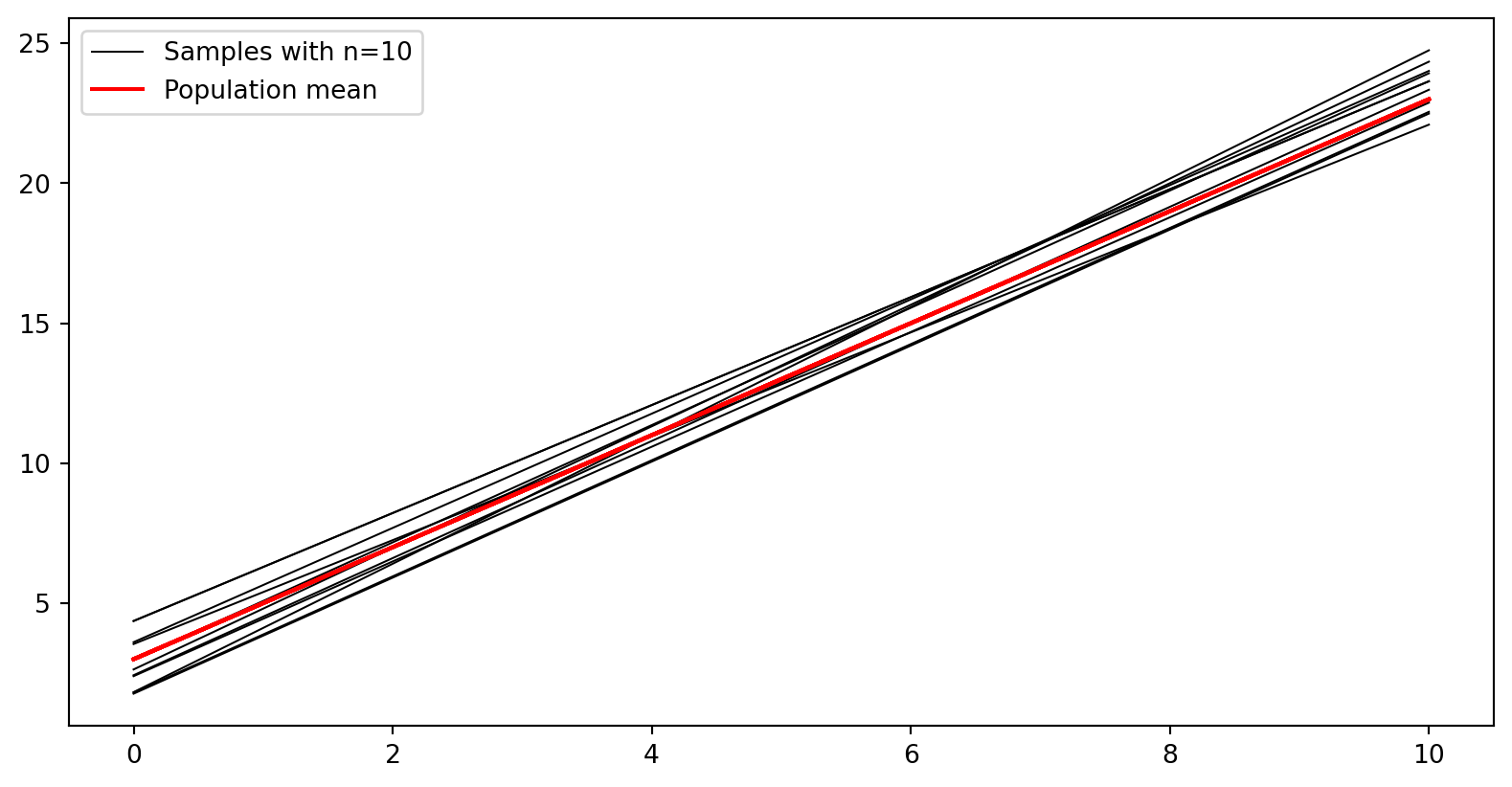
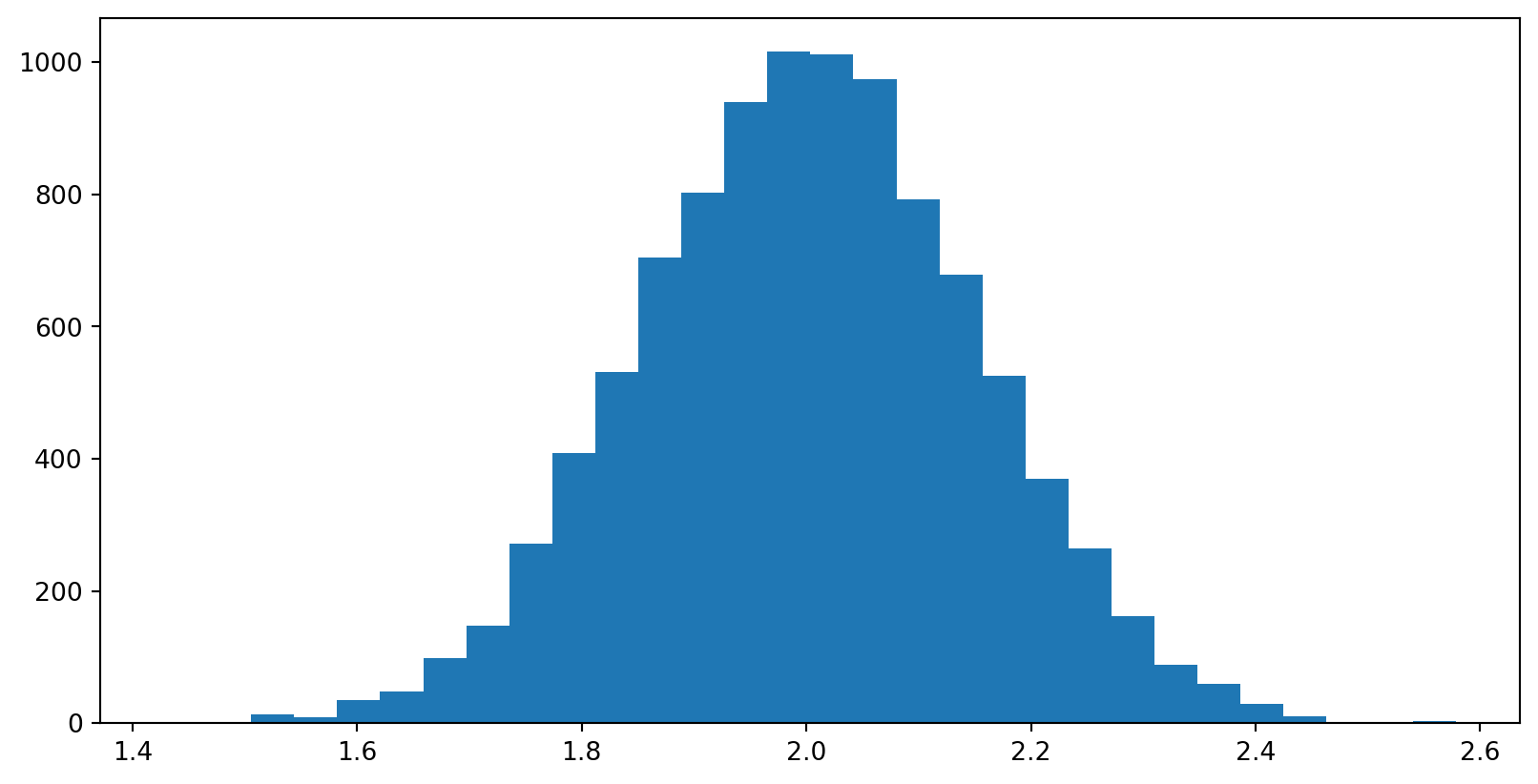
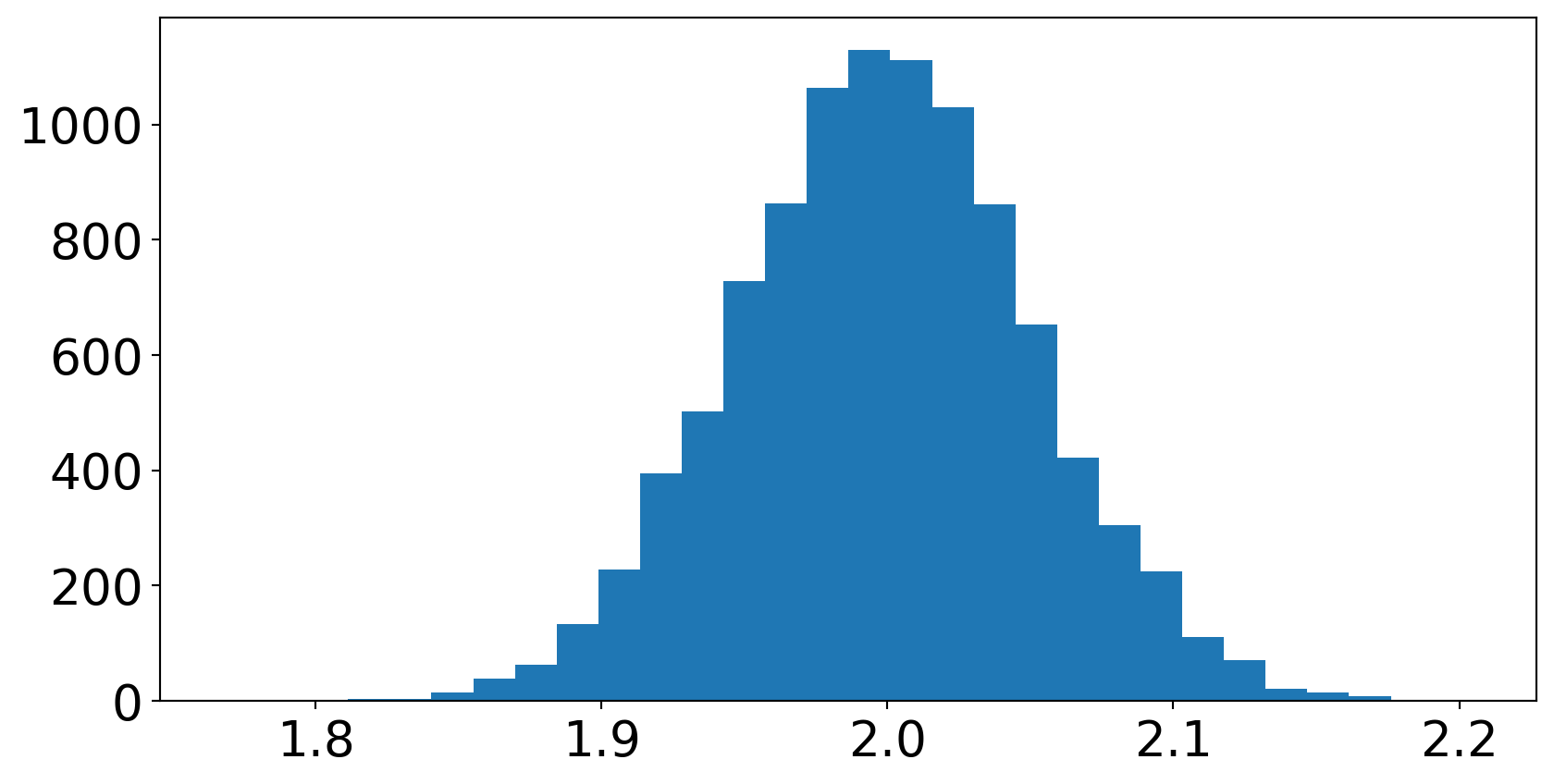
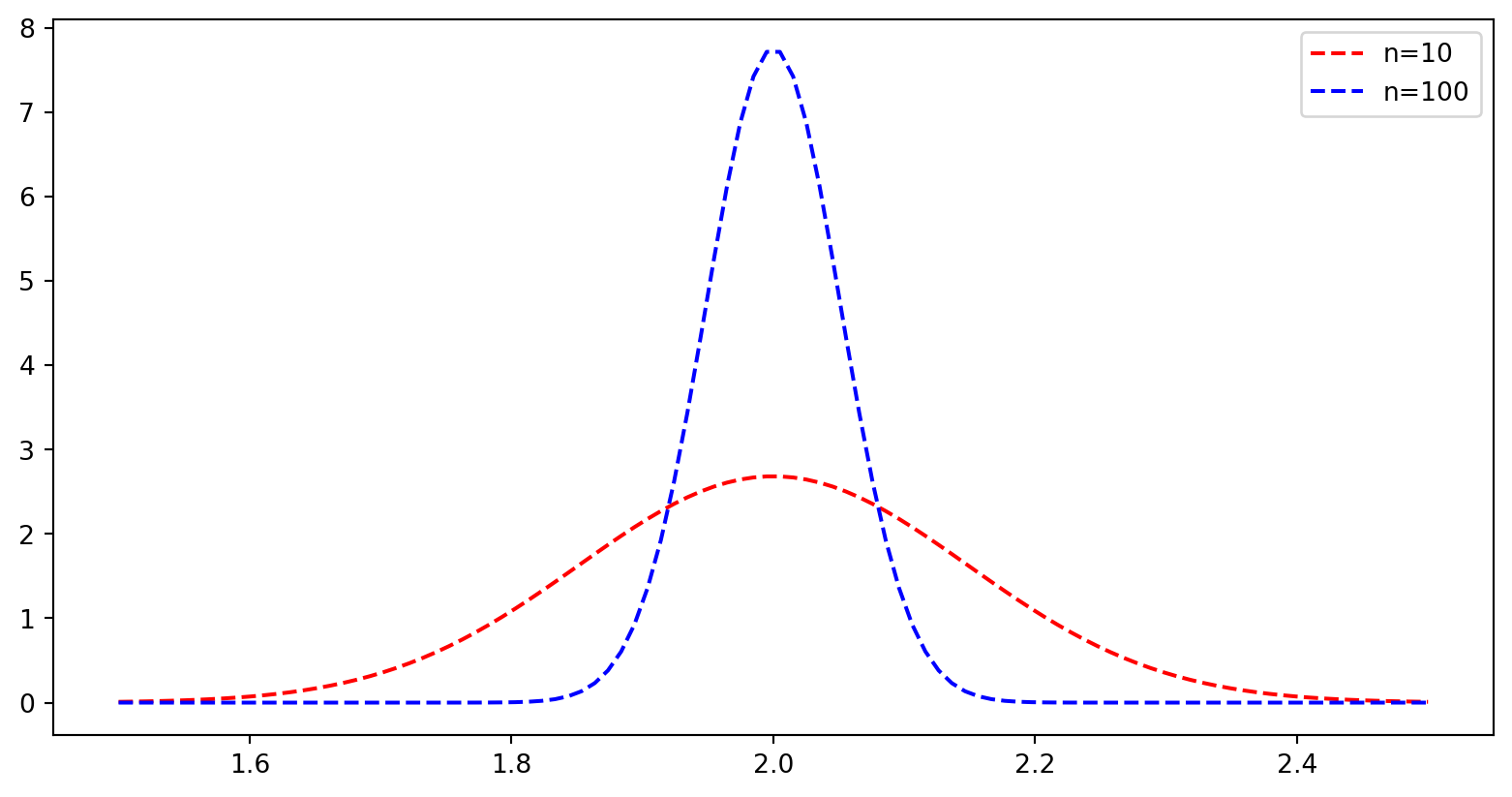
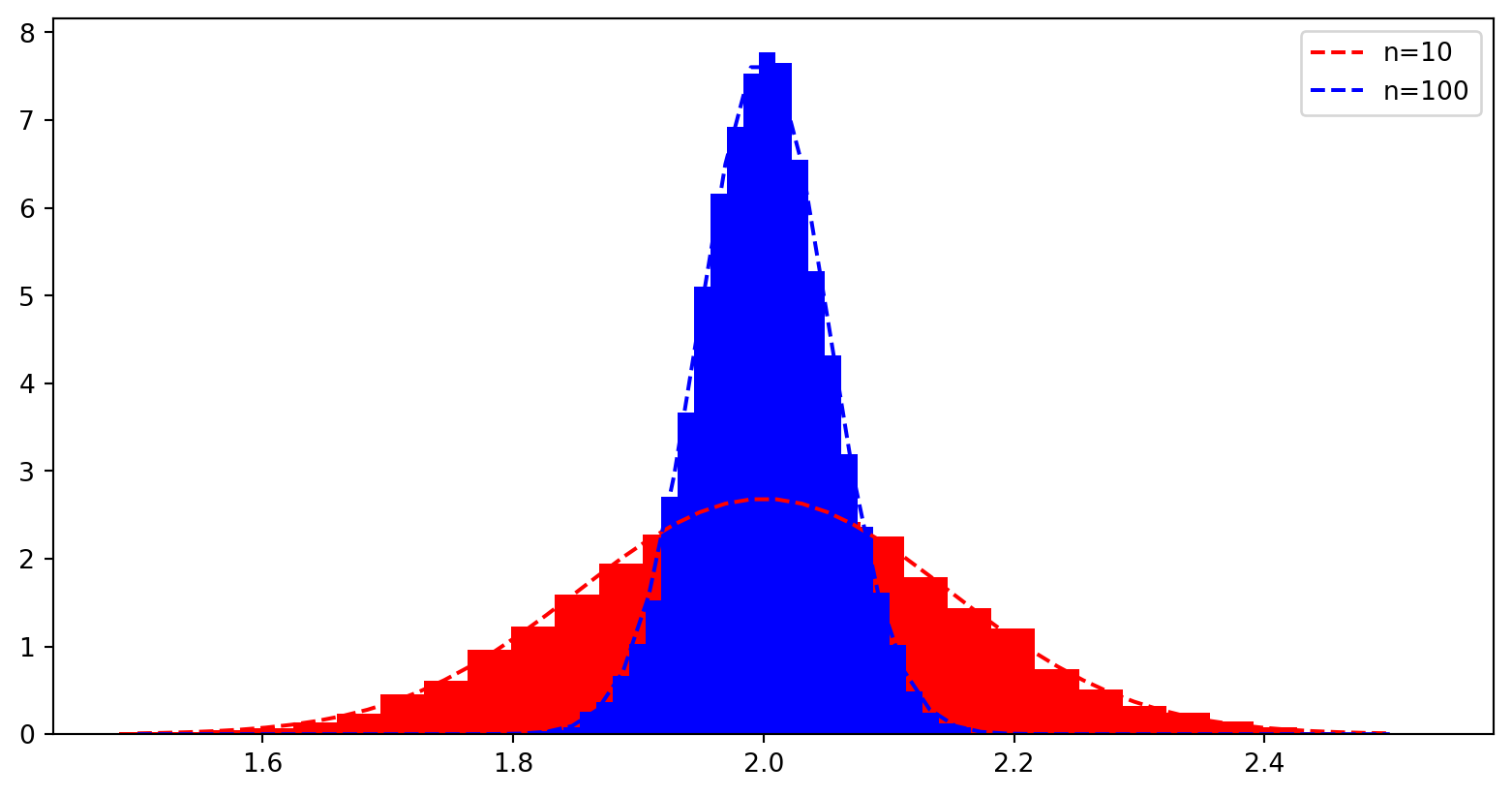
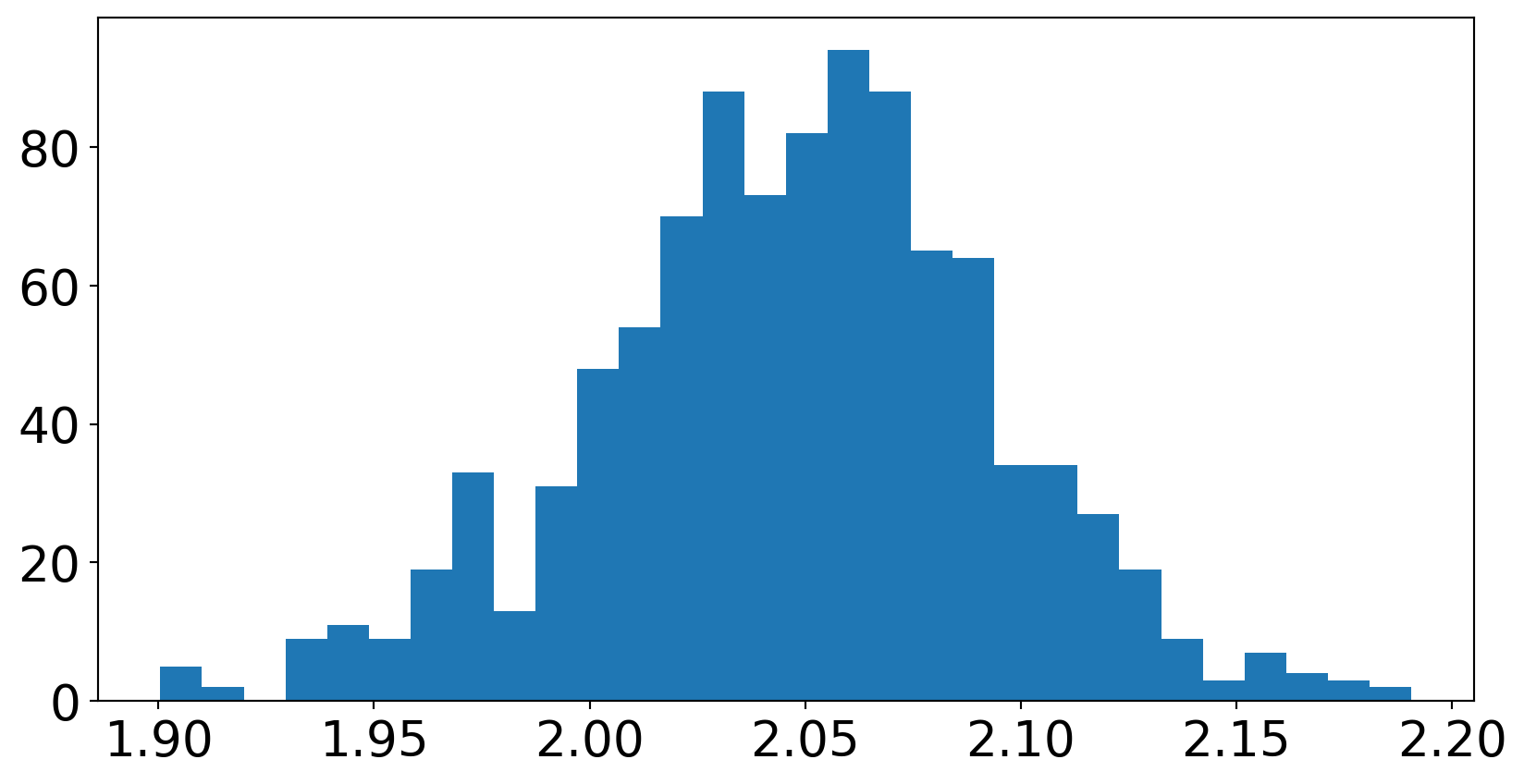
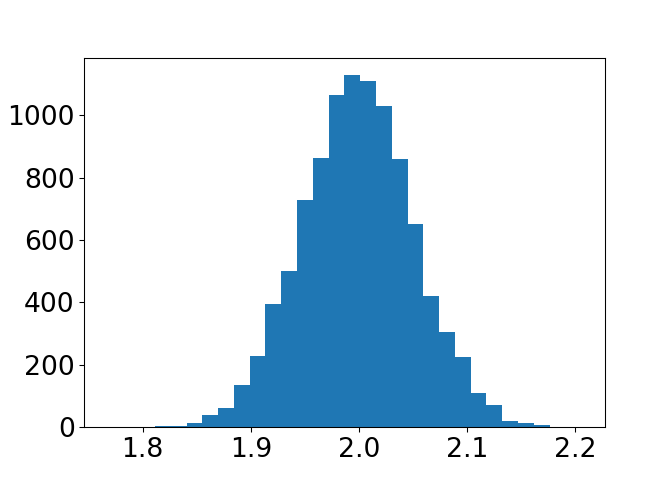
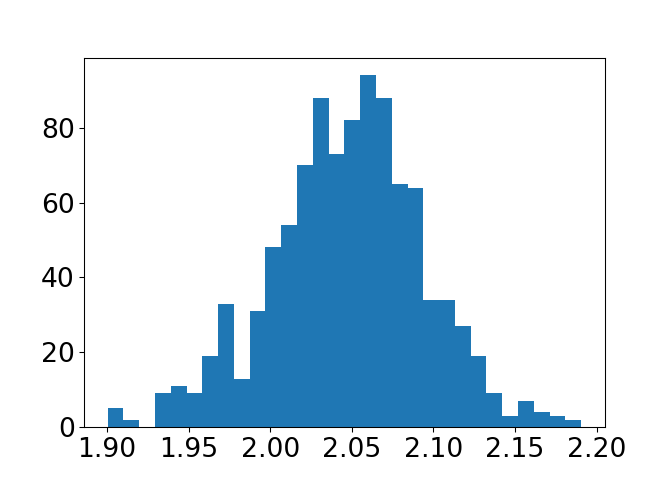
c) Gjenta mange ganger (f. eks 10000 i en for-løkke), og lagre stigningstallet som estimeres for hver enkelt linje. Plott et histogram over stigningstallene, med plt.hist.

Løsningsforslag a og b

def f(x): 
    return 2*x + 3

x = np.linspace(0, 10, 10)
y = f(x) + np.random.normal(0, 1.5, 10)
p = np.polyfit(x, y, 1)
y_hat = np.polyval(p, x)
plt.plot(x, y, "o")
plt.plot(x, y_hat)

Løsningforslag c

<Figure size 960x480 with 0 Axes>

N = 10000
slopes = []
for i in range(N):
    x = np.linspace(0, 10, 10)
    y = f(x) + np.random.normal(0, 1.5, 10)
    p = np.polyfit(x, y, 1)
    slopes.append(p[0])
_ = plt.hist(slopes, bins=30)

Øke antallet punkter til 100

N = 10000
slopes = []
for i in range(N):
    x = np.linspace(0, 10, 100)
    y = f(x) + np.random.normal(0, 1.5, 100)
    p = np.polyfit(x, y, 1)
    slopes.append(p[0])
_ = plt.hist(slopes, 30)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.savefig("figures/est_beta1.png")

Hva skjedde med fordelingen av stigningstall?

Tolkning

Kort diskusjonsoppgave

a) Hva skjedde med fordelingen av stigningstall ved lineær regresjon da vi økte fra 10 til 100 punkter?

b) Hvordan skal vi tolke dette?

Feilestimat

Fra boka har vi følgende formel for forventet feil i stigningtallet: \[\mathrm{SE}(\hat{\beta}_1) = \sqrt{\frac{\sigma^2}{\sum_{i=1}^n(x_i-\bar{x})^2}}\]

der \(\sigma\) er standardavviket til den tilfeldige variablen \(\varepsilon\) i \(y = f(x) + \varepsilon\)

Anvendt på våre tall

Vi trakk tilfeldige tall med \(\sigma=1.5\) og hhv. 10 og 100 jevnt fordelte tall fra 0 til 10. Altså:

x = np.linspace(0, 10, 10)
se = np.sqrt(1.5**2/np.sum((x-np.mean(x))**2))
print(f"Standard feil for n=10: {se}")

x = np.linspace(0, 10, 100)
se = np.sqrt(1.5**2/np.sum((x-np.mean(x))**2))

print(f"Standard feil for n=100: {se}")

Standard feil for n=10: 0.1486301082920587
Standard feil for n=100: 0.051444481273168134

Normalfordelinger med disse parametrene:

Normalfordelinger sammen med datasettene

Men om vi har målt noe, så har vi jo bare én måleserie. Hva kan vi gjøre da?

Bootstrap

np.random.seed(16)
x = np.linspace(0, 10, 100)
y = f(x) + np.random.normal(0, 1, 100)
slopes = []
for i in range(1000):
    selection = np.random.randint(0, len(x), 50)
    x_c = x[selection]
    y_c = y[selection]
    p = np.polyfit(x_c, y_c, 1)
    slopes.append(p[0])
_ = plt.hist(slopes, bins=30)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.savefig("figures/est_bootstrap.png")

Tolkning

Note

Se nøye på figurene, hva skjer her?

Om tid

• Begynne på ukesoppgavene