Forelesningsnotat: Trening, testing, kryssvalidering, overtrening

Henrik Sveinsson

Slide-versjon

Premiss

Jeg har laget meg en funksjon som er på formen

\[p(x) = c_0 + c_1 x + c_2x^2 + \cdots = \sum_{i=0}^\infty c_i x^i\]

Så har jeg trukket noen tall \(y = p(x) + \varepsilon\), der verdiene \(\varepsilon\) er normalfordelt.

Men jeg holder c´ene hemmelige for dere, og jeg holer standardavviket i normalfordelingen hemmelig for dere.

Datasettet

Dette er slik det datasettet jeg har trukket ser ut:

Det kan lastes ned her.

Overordnet oppgave for økta

Finne best mulig estimat for \(\{c_i\}\). Dette innebærer i hovedsak å finne ut hvor høye \(i\) vi skal gå til, altså hvor store polynomer.

Lese inn datasettet:

import numpy as np
data = np.loadtxt("data/hemmelig_funksjon.txt")
print(data)
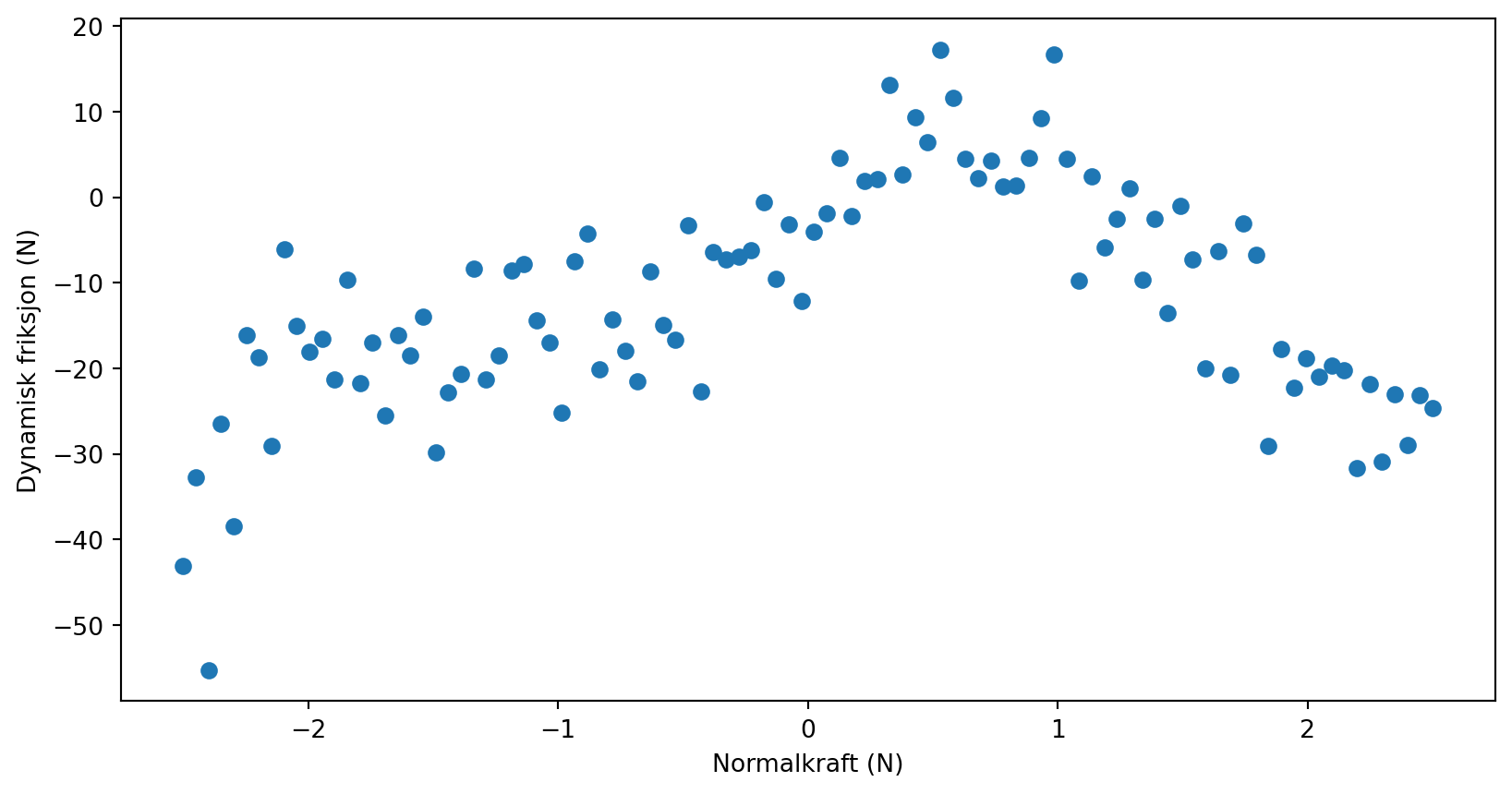
x = data[:,0]
y = data[:,1]

[[-2.50000000e+00 -4.30998734e+01]
 [-2.44949495e+00 -3.26987345e+01]
 [-2.39898990e+00 -5.52854260e+01]
 [-2.34848485e+00 -2.64284688e+01]
 [-2.29797980e+00 -3.84960068e+01]
 [-2.24747475e+00 -1.60790906e+01]
 [-2.19696970e+00 -1.86770254e+01]
 [-2.14646465e+00 -2.91149443e+01]
 [-2.09595960e+00 -6.11836062e+00]
 [-2.04545455e+00 -1.50227974e+01]
 [-1.99494949e+00 -1.81119780e+01]
 [-1.94444444e+00 -1.65905377e+01]
 [-1.89393939e+00 -2.12568736e+01]
 [-1.84343434e+00 -9.62635475e+00]
 [-1.79292929e+00 -2.17751798e+01]
 [-1.74242424e+00 -1.70026584e+01]
 [-1.69191919e+00 -2.55251597e+01]
 [-1.64141414e+00 -1.61060757e+01]
 [-1.59090909e+00 -1.85088369e+01]
 [-1.54040404e+00 -1.40123432e+01]
 [-1.48989899e+00 -2.97722450e+01]
 [-1.43939394e+00 -2.28487165e+01]
 [-1.38888889e+00 -2.06196657e+01]
 [-1.33838384e+00 -8.34302038e+00]
 [-1.28787879e+00 -2.12597816e+01]
 [-1.23737374e+00 -1.85375108e+01]
 [-1.18686869e+00 -8.51863427e+00]
 [-1.13636364e+00 -7.84281649e+00]
 [-1.08585859e+00 -1.43893080e+01]
 [-1.03535354e+00 -1.70080645e+01]
 [-9.84848485e-01 -2.52287943e+01]
 [-9.34343434e-01 -7.46827788e+00]
 [-8.83838384e-01 -4.20727167e+00]
 [-8.33333333e-01 -2.01172945e+01]
 [-7.82828283e-01 -1.42435178e+01]
 [-7.32323232e-01 -1.79813866e+01]
 [-6.81818182e-01 -2.15525632e+01]
 [-6.31313131e-01 -8.62162620e+00]
 [-5.80808081e-01 -1.48933104e+01]
 [-5.30303030e-01 -1.66653963e+01]
 [-4.79797980e-01 -3.26441443e+00]
 [-4.29292929e-01 -2.27294730e+01]
 [-3.78787879e-01 -6.39051535e+00]
 [-3.28282828e-01 -7.26030695e+00]
 [-2.77777778e-01 -6.91538326e+00]
 [-2.27272727e-01 -6.16544677e+00]
 [-1.76767677e-01 -5.84873488e-01]
 [-1.26262626e-01 -9.57800773e+00]
 [-7.57575758e-02 -3.13795504e+00]
 [-2.52525253e-02 -1.20919746e+01]
 [ 2.52525253e-02 -3.97828128e+00]
 [ 7.57575758e-02 -1.89130952e+00]
 [ 1.26262626e-01  4.55607660e+00]
 [ 1.76767677e-01 -2.20442195e+00]
 [ 2.27272727e-01  1.85921687e+00]
 [ 2.77777778e-01  2.15298119e+00]
 [ 3.28282828e-01  1.31827583e+01]
 [ 3.78787879e-01  2.67761036e+00]
 [ 4.29292929e-01  9.30574969e+00]
 [ 4.79797980e-01  6.47882568e+00]
 [ 5.30303030e-01  1.72505807e+01]
 [ 5.80808081e-01  1.15839155e+01]
 [ 6.31313131e-01  4.53477786e+00]
 [ 6.81818182e-01  2.25102486e+00]
 [ 7.32323232e-01  4.33169718e+00]
 [ 7.82828283e-01  1.31314261e+00]
 [ 8.33333333e-01  1.35134770e+00]
 [ 8.83838384e-01  4.61298306e+00]
 [ 9.34343434e-01  9.23672856e+00]
 [ 9.84848485e-01  1.66842812e+01]
 [ 1.03535354e+00  4.48689914e+00]
 [ 1.08585859e+00 -9.74590045e+00]
 [ 1.13636364e+00  2.40751597e+00]
 [ 1.18686869e+00 -5.86980559e+00]
 [ 1.23737374e+00 -2.52396593e+00]
 [ 1.28787879e+00  1.04290087e+00]
 [ 1.33838384e+00 -9.60840164e+00]
 [ 1.38888889e+00 -2.49422729e+00]
 [ 1.43939394e+00 -1.35700524e+01]
 [ 1.48989899e+00 -1.01926018e+00]
 [ 1.54040404e+00 -7.29316159e+00]
 [ 1.59090909e+00 -1.99989544e+01]
 [ 1.64141414e+00 -6.33228306e+00]
 [ 1.69191919e+00 -2.07056401e+01]
 [ 1.74242424e+00 -3.01512622e+00]
 [ 1.79292929e+00 -6.76592729e+00]
 [ 1.84343434e+00 -2.90505187e+01]
 [ 1.89393939e+00 -1.77320961e+01]
 [ 1.94444444e+00 -2.22495263e+01]
 [ 1.99494949e+00 -1.88432281e+01]
 [ 2.04545455e+00 -2.10084218e+01]
 [ 2.09595960e+00 -1.97315339e+01]
 [ 2.14646465e+00 -2.01852203e+01]
 [ 2.19696970e+00 -3.16092294e+01]
 [ 2.24747475e+00 -2.18156289e+01]
 [ 2.29797980e+00 -3.09277432e+01]
 [ 2.34848485e+00 -2.29934136e+01]
 [ 2.39898990e+00 -2.89183290e+01]
 [ 2.44949495e+00 -2.31338756e+01]
 [ 2.50000000e+00 -2.46218930e+01]]

Tilfeldig gjettet \(i_\mathrm{max}\)

p = np.polyfit(x, y, 3)
x_v = np.linspace(-2.5, 2.5, 100)
plt.plot(x, y, "o")
plt.plot(x_v, np.polyval(p, x_v))

Test av forskjellige polynomer

Vi skjønner kanskje at vi må stoppe et sted, men hvor?

Vi må bruke noen systematiske verktøy for å klare å ta en god beslutning om hvor vi skal stoppe polynomet vårt!

Mean squared error

Vi har et datasett med verdier \(\{x_i, y_i\}\). Vi lager oss et polynom \(p(x)\), som vi bruker til å estimere y-verdier, altså \(\hat{y} = f(x)\).

Vi ønsker å minimere

\[\sum_{i=1}^N (\hat{y}_i - y_i)^2 = \sum_{i=1}^N (f(x_i) - y_i)^2\]

Mean squared error

Underveisoppgave

• Last inn datasettet trukket fra den hemmelige fordelingen.
• Plott datasettet for å verifisere at det er korrekt innlest.
• Gjør polynomtilpasning med \(p(x)=\sum_{i=0}^N c_i x^i\) for \(N\) opp til \(20\). Plott de forskjellige polynomene på intervallet \([-2.5, 2.5]\)
• Finn treningsfeilen, altså \(\sum_{i=0}^n (p(x_i)-y_i)^2\), for hver polynomgrad N, og plott feilen som funksjon av N.

Starthjelp

data = np.loadtxt("data/hemmelig_funksjon.txt")
x = data[:,0]
y = data[:,1]
for i in range(1,15):
    p = np.polyfit(x, y, i)

Løsning

plt.subplot(1,2,1)
plt.plot(x,y, "o")

N = 5
training_errors = np.zeros(N+1)
for i in range(N+1):
    p = np.polyfit(x, y, i)
    xv = np.linspace(-2.5, 2.5, 200)
    plt.subplot(1,2,1)
    plt.plot(xv, np.polyval(p, xv), c=get_color_value(i, 0, N, cmap="jet"), label=f"{i}")
    training_errors[i] = np.mean((np.polyval(p, x)-y)**2)

plt.legend()
plt.subplot(1,2,2)
plt.plot(training_errors)
plt.xlabel("Grad av polynom")
plt.ylabel("Treningsfeil")
plt.tight_layout()

Løsning

Øke N

• Hva kan vi lære om hvilken N vi bør velge av dette?

Validerings-trenings-splitt 50/50

• Vi deler datasettet i to deler, hvorfor det?

• Avdekke overtilpasning
• Vurdere modellkvalitet
• Velge modell

Implementasjonsforslag for datasplitting

indices = np.random.permutation(len(x))
idx_train, idx_validate = np.array_split(indices, 2)
x_train = x[idx_train]
y_train = y[idx_train]
x_validate = x[idx_validate]
y_validate = y[idx_validate]

Vi deler opp datasettet i treningssett og valideringssett for å kunne evaluere modellen på data som den ikke har sett under trening. Treningssettet brukes til å trene modellen, mens valideringssettet brukes til å bestemmehvor høye grads polynomer vi kan ta med i modellen uten å få overtilpasning.

Oppgave

• Print indeksene for treningsdata og valideringsdata.
• Verifiser (med programmering) at indeksene i treningsdata og valideringsdata er forskjellige.
• Plott treningsdata og valideringsdata i forskjellige farger for å verifisere at de er tilfeldig, og ikke systematisk, trukket!

Løsning

import matplotlib.pyplot as plt 

plt.plot(x_train, y_train, "o", label="treningsdata")
plt.plot(x_validate, y_validate, "o", label="testdata")
plt.legend()

Test-train-split 50/50

• Nå ønsker vi å sammenligne gjennomsnittlig kvadrert feil for treningsdata og valideringsdata ved forskjellige valg av høyeste mulige grad av polynom, for eksempel om vi setter høyeste grad til 20 har vi: \[p(x) = \sum_{i=0}^{20} c_i x^i\]

Oppgave

• Skriv opp hvordan vi konseptuelt kan gjøre dette

Implementasjon

(her skal vi gå igjennom koden linje for linje! Rop om jeg ikke gjør det)

plt.subplot(1,2,1)
plt.plot(x,y, "o")

N = 15
training_errors = np.zeros(N+1)
validation_errors = np.zeros(N+1)
for i in range(N+1):
    p = np.polyfit(x_train, y_train, i)
    xv = np.linspace(-2.5, 2.5, 200)
    plt.subplot(1,2,1)
    plt.plot(xv, np.polyval(p, xv), c=get_color_value(i, 0, N, cmap="jet"), label=f"{i}")
    training_errors[i] = np.mean((np.polyval(p, x_train)-y_train)**2)
    validation_errors[i] = np.mean((np.polyval(p, x_validate)-y_validate)**2)

plt.subplot(1,2,2)
plt.plot(training_errors, label="training error")
plt.plot(validation_errors, label="test error")
plt.xlabel("Grad av polynom")
plt.ylabel("Treningsfeil")
plt.legend()
plt.tight_layout()

• Hva lærte vi nå om hvilken polynomgrad vi bør bruke?

Implementasjon

Foreløpig oppsummering

• Vi har funnet ut at et polynom av grad mellom 3 og 8 bør kunne funke. Kan vi gjøre det bedre?

k-fold kryssvalidering!

Fold	Partisjon 1	Partisjon 2	Partisjon 3	Partisjon 4	Partisjon 5
1	🟥 Validering	🟦 Trening	🟦 Trening	🟦 Trening	🟦 Trening
2	🟦 Trening	🟥 Validering	🟦 Trening	🟦 Trening	🟦 Trening
3	🟦 Trening	🟦 Trening	🟥 Validering	🟦 Trening	🟦 Trening
4	🟦 Trening	🟦 Trening	🟦 Trening	🟥 Validering	🟦 Trening
5	🟦 Trening	🟦 Trening	🟦 Trening	🟦 Trening	🟥 Validering

Oppgave

Dere skal nå dele opp datasettet i 5 partisjoner, og verifiser med et plott at det har gått bra.

Beskriv først med ord hva som skal til for å dele opp i 5 partisjoner.

Dette er slik vi delte i treningsdata og valideringsdata tidligere:

indices = np.random.permutation(len(x))
idx_train, idx_validate = np.array_split(indices, 2)
x_train = x[idx_train]
y_train = y[idx_train]
x_validate = x[idx_validate]
y_validate = y[idx_validate]

Løsning

np.random.seed(0)
indices = np.random.permutation(len(x))
partitions = np.array_split(indices, 5)

colors = ["r", "g", "b", "c", "m"]
plt.figure(figsize=(8, 4))
for i, partition in enumerate(partitions):
    plt.plot(x[partition], y[partition], "o", label=f"Partisjon {i+1}", color=colors[i])
plt.legend()

Dele opp i 5 folds

Det er kanskje ikke helt åpenbart, men det å dele opp i 5 folds er ikke det samme som å dele opp i 5 partisjoner.

Oppgave

Del opp i 5 partisjoner, og visualier disse partisjonene.

(Live-programmere løsning)

Tilpasse polynom til hver fold

fig, axs = plt.subplots(2, 3, figsize=(9, 6), sharey=True)
axs = axs.flatten()

for i, partition in enumerate(partitions):
    train_idx = np.setdiff1d(indices, partition)
    p = np.polyfit(x[train_idx], y[train_idx], 4)
    axs[i].plot(x[train_idx], y[train_idx], "o", color="lightgray", label="Treningsdata")
    axs[i].plot(x[partition], y[partition], "o", color="blue", label="Valideringsdata")
    xv = np.linspace(-2.5, 2.5, 100)
    yv = np.polyval(p, xv)
    axs[i].plot(xv, yv, "k")
    axs[5].plot(xv, yv)
    axs[i].set_title(f"Fold {i+1}")
    axs[i].legend()
plt.tight_layout()

Hvilke data er det linja er tilpasset til i grafene over her. Er det de grå eller de blå? Hva er fold og hva er partisjoner her?

I denne tilpasningen har jeg brukt et polynom av grad 4. Hva skal vi gjøre for å beregne mean squared error for den et polynom av grad 4 med 5-fold kryssvalidering? Beskriv på figuren.

Tilpasse polynom til hver fold

Tilfellet \(i_\mathrm{max}=4\)

mean_squared_error = 0
for i, partition in enumerate(partitions):
    train_idx = np.setdiff1d(indices, partition)
    p = np.polyfit(x[train_idx], y[train_idx], 4)
    mean_squared_error += np.mean((np.polyval(p, x[partition])-y[partition])**2)
mean_squared_error /= len(partitions)
print(mean_squared_error)

70.96934537774104

Snitt av alle folds, for mange \(i_\mathrm{max}\)

Vi ønsker nå å bruke k-fold kryssvalidering til å sammenligne hvor bra modellene blir med forskjellige valg av \(i_\mathrm{max}\).

Snitt av alle folds, for mange \(i_\mathrm{max}\)

folds = np.array_split(indices, 5)

i_max = 15
mse_values = np.zeros(15)

for i, fold in enumerate(folds):
    train_idx = np.setdiff1d(indices, fold)
    for j in range(i_max):
        p = np.polyfit(x[train_idx], y[train_idx], j)
        mse = np.mean((np.polyval(p, x[fold])-y[fold])**2)
        mse_values[j] += mse 
mse_values /= len(folds)
plt.plot(mse_values)
plt.plot([0, 10], [49, 49], "--", c="k")

Den stiplede linja avslører den ekte variansen til det stokastiske leddet \(\varepsilon\) fra datatrekningen i starten av timen.

Snitt av alle folds, for mange \(i_\mathrm{max}\)

Peker mot \(i_\mathrm{max} = 5?\)

[-3.39655030e+00  2.82703972e+01  8.67920082e+00 -3.31733925e+01
 -1.86241023e+01  1.52155891e+01  1.09424134e+01 -1.25976127e+00
 -3.59182687e+00 -9.53165305e-01  7.60116699e-01  2.49178868e-01
 -9.66010793e-02 -1.72214555e-02  5.26860717e-03]

Sammenligning av \(\{c_i\}\)

Fasit: [0, 20, -8, -10.7, 1.2, 1.6, -0.15, -0.05]
Beste modell:  [ 1.15123423 -0.15289326 -9.51306655 -4.00555715 18.74401723 -2.10654956]
Beste modell når vi kjenner $i_{max}$:  [ -0.03446598  -0.13178075   1.50576443   0.99185812 -10.53909373
  -6.43603876  19.46976614  -1.369465  ]

Merk at selv med 100 punkter fikk vi ganske dårlige estimater på \(c\)-verdiene. Om disse verdiene er viktige å vite nøyaktig for å karakterisere et eller annet system eller fenomen, så må vi være klar over at selv om modellen ser ut til å prestere bra, så trenger ikke alt å være presist. Vi kom nesten helt ned på samme variasjon fra modellen til dataene som det som lå i selve trekkingen av data. Men allikevel er avviket på enkeltkoeffisientene stort.

Måter å gjøre ting enklere på

I stedet for np.array_split manuelt, kan vi kjøre

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.5, random_state=0)

plt.plot(x_train, y_train, "o", label="train")
plt.plot(x_test, y_test, "o", label="validation")
plt.legend()

Måter å gjøre ting enklere på

For kryssvalidering kan vi i stedet for np.array_split kjøre sklearn.model_selection.KFold.

from sklearn.model_selection import KFold

kf = KFold(n_splits=5)
for train_index, validate_index in kf.split(range(len(x))):
    plt.plot(x[validate_index], y[validate_index], "o")

• Men obs!

Måter å gjøre ting enklere på

Måter å gjøre ting enklere på

Må passe på at autometodene ikke lurer oss! Her måtte vi oppgi at dataene skulle stokkes, siden de var sortert etter x-aksen fra før.

from sklearn.model_selection import KFold

kf = KFold(n_splits=5, shuffle=True)
for train_index, validate_index in kf.split(range(len(x))):
    plt.plot(x[validate_index], y[validate_index], "o")

Måter å gjøre ting enklere på

Kryssvalidering

Vi bruker kryssvalidering for å

1. Hindre overtilpasning. Om testfeilen er mye større enn treningsfeilen har vi typisk overtilpasset
2. Utnytte data godt. Kryssvalidering gir et godt estimat på hva som er usikkerheten når vi trener på alle dataene våre.

Hvorfor k-fold, og ikke leave one out kryssvalidering?

Eksempel på k-fold kryssvalidering med k=5:

Fold 1: Train on [2, 3, 4, 5], Test on [1]
Fold 2: Train on [1, 3, 4, 5], Test on [2]
Fold 3: Train on [1, 2, 4, 5], Test on [3]
Fold 4: Train on [1, 2, 3, 5], Test on [4]
Fold 5: Train on [1, 2, 3, 4], Test on [5]