Forelesningsnotat: Logistisk regresjon

Modellering med én forklaringsvariabel

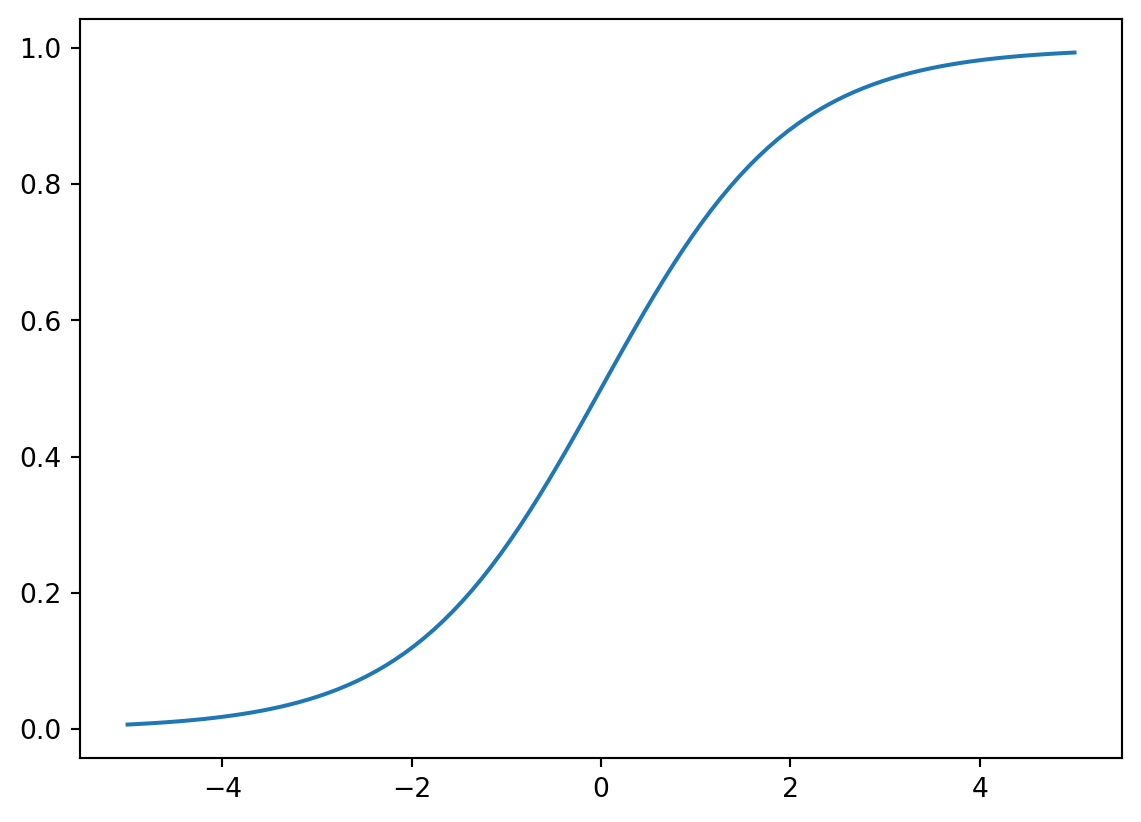
\[y = f(x) + \varepsilon\]

Der \(f(x)\) er det vi greier å forklare med modellen vår, og \(\varepsilon\) er det vi ikke klarer å forklare.

Vi gjør prediksjoner med

\[ \hat y = f(x) \]

Og kaller da \(\hat y\) for “estimert y”

Forrige uke

Vi så på

\[ f(x) = ax + b \]

Og anvendte dette på fiktive målinger for Ohms lov:

\[ I(U) = \frac{1}{R} U\]

som er \(ax + b\), men med \(a=\frac{1}{R}\), \(b=0\) og den generelle forklaringsvariablen som generelt heter \(x\) heter heller \(U\) når den beskriver strøm.

I dag

• Sigmoid-fuksjonen \(f(z)=\frac{e^z}{1+e^z}\)
• Utvidelse til \(z = \beta_0 + \beta_1 x\), hvordan påvirkes sigmoiden av \(\beta_0\) og \(\beta_1\)?
• Regresjon med sigmoidfunksjon.
• Flere forklaringsvariable: \(z = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots\)
• Funksjonstilpasning med flere variable

Sigmoidfunksjonen

\[ f(z) = \frac{e^z}{1+e^z} \]

Hvordan ser denne funksjonen ut?

Underveisoppgave

• Hva er \(f(0)\)?
• Hva er \(f(-\infty)\)?
• Hva er \(f(\infty)\)? Tegn opp funksjonen

Sigmoidfunksjonen

import numpy as np
def f(z): 
    return np.exp(z)/(1 + np.exp(z))

z = np.linspace(-5, 5, 100)
import matplotlib.pyplot as plt 
plt.plot(z, f(z))

Modell for nedbør

Oppgave

import numpy as np
def f(z): 
    return np.exp(z)/(1 + np.exp(z))

z = np.linspace(-5, 5, 100)
import matplotlib.pyplot as plt 
plt.plot(z, f(z))
plt.xlabel("Temperatur (celsius)")
_= plt.ylabel("Nedbør som regn?")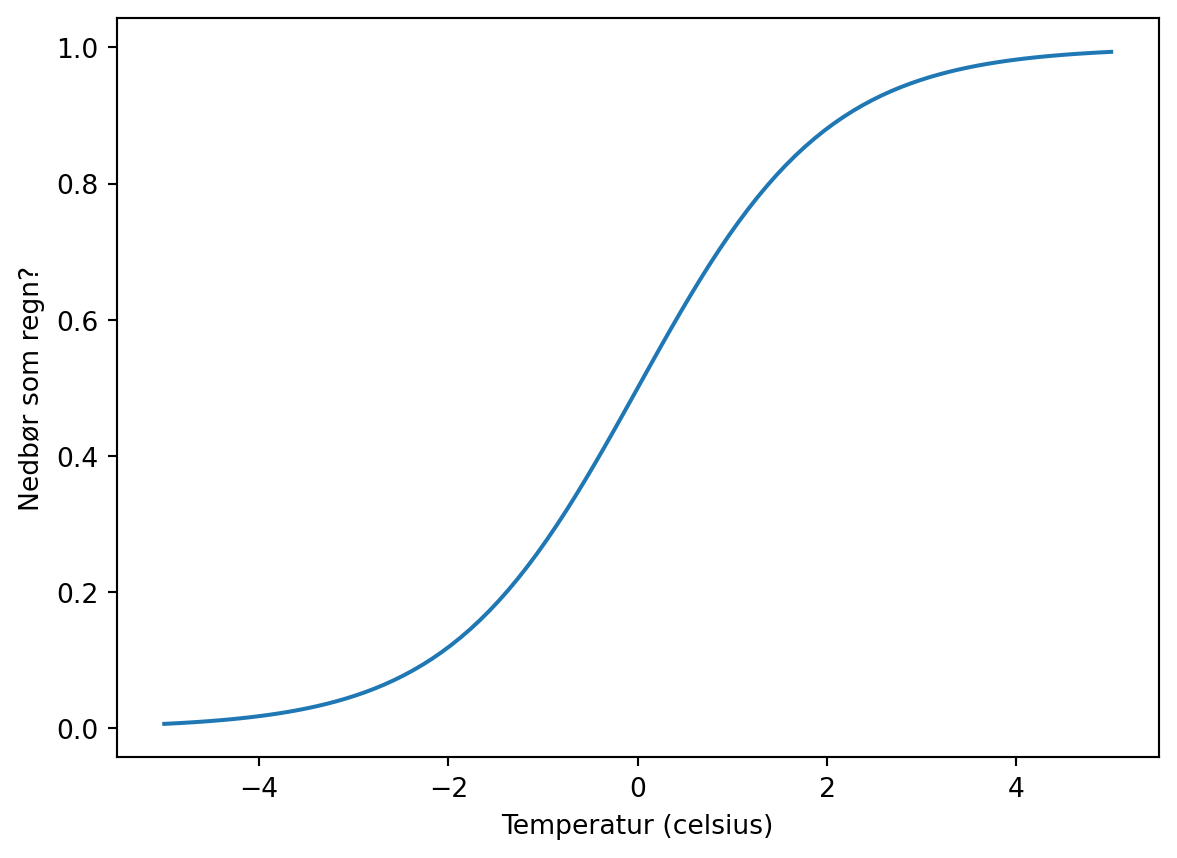

• Hvorfor er dette en meningsfull modell for hvorvidt nedbør kommer som regn?
• Men stemmer det helt?

Det snør gjerne også litt over null grader.

Komplisere \(z\) i \(f(z)\)

Sette \(z = \beta_0 + \beta_1 x\).

Da kan vi heller lage oss \(p(x) = \frac{e^{\beta_0 + \beta_1 x}}{1 + e^{\beta_0 + \beta_1 x}}\)

Shift

Ny modell for nedbør

• Hvordan bør vi sette \(\beta_0\) for å lage en fornuftig modell for nedbør?

Vi har bare gjettet

• Hvordan ville du gå fram hvis du skulle lage en slik modell, og det var viktig at den fungerte?

Hva kan være viktig

• Om du er kredittkortselskap er det viktig at kundene betaler for seg (ikke med en gang), men til slutt, de bør ikke misligholde.

Default-datasettet

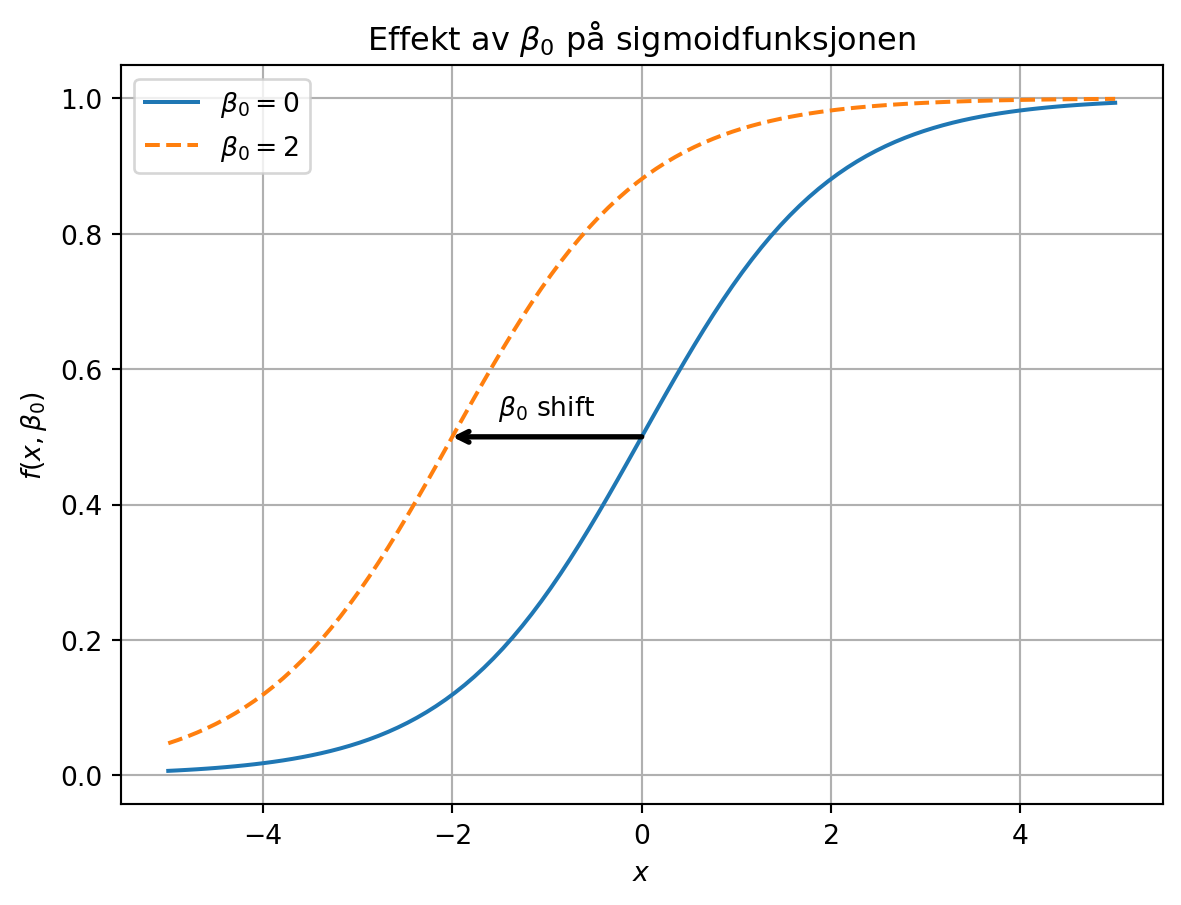
Vi gjør en egen tutorial som handler om dette datasettet, for å få litt praktisk omgang med logistisk regresjon!