Forelesningsnotat – Obligatorisk oppgave

Titanic

I filmen om titanic-forliset følger overlevelsen det mønsteret man godt kunne tenke seg. Kvinner på første klasse overlever, og menn på tredje klasse dør. Hvem hvor godt klarer vi å bruke det vi vet om en passaser til å predikere om vedkommende kommer til å overleve titanic-forliset? og kan vi bruke en slik modell til å forstå noe om hvordan de forskjellige egenskapene til en person, slik som kjønn, alder og pris på billetten, påvirker overlevelsen ved et forlis?

Men før det

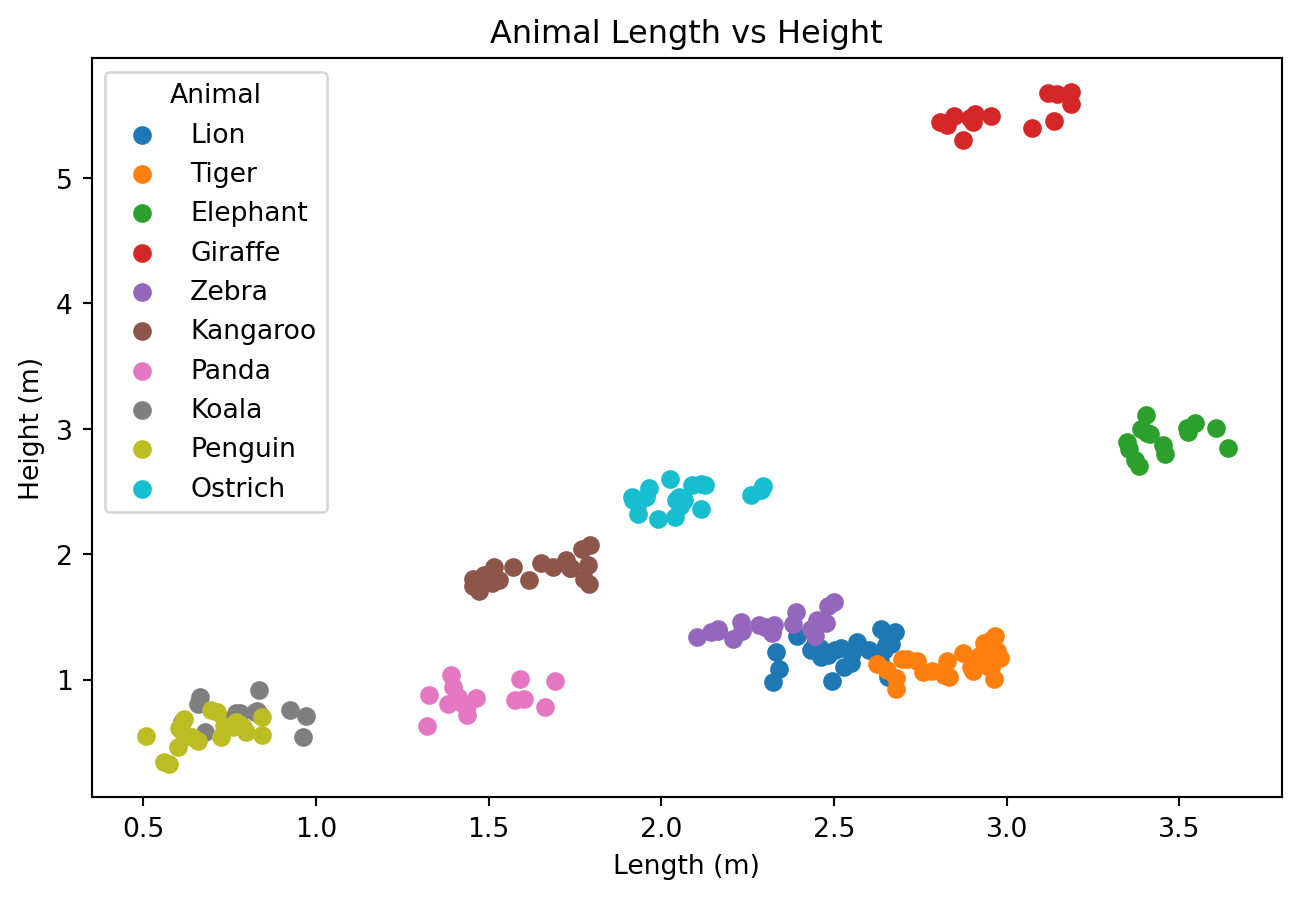
• Høyde og lengde på forskjellige dyr

	Animal	Length	Height
93	Zebra	2.499837	1.621510
17	Lion	2.632459	1.147693
167	Penguin	0.798167	0.585082
60	Elephant	3.388946	2.996978
148	Koala	0.769779	0.730835
127	Panda	1.438418	0.790432
45	Tiger	2.919400	1.186447
16	Lion	2.502121	1.233868

Vi har laget oss et datasett med lengde- og høydedata om forskjellige dyr. Det kan lastes ned her.

Plot

import matplotlib.pyplot as plt
# Load the dataset from the CSV file
animal_data = pd.read_csv('data/animal_data.csv')
plt.figure(figsize=(8, 5))
plt.plot(animal_data["Length"], animal_data["Height"], "o")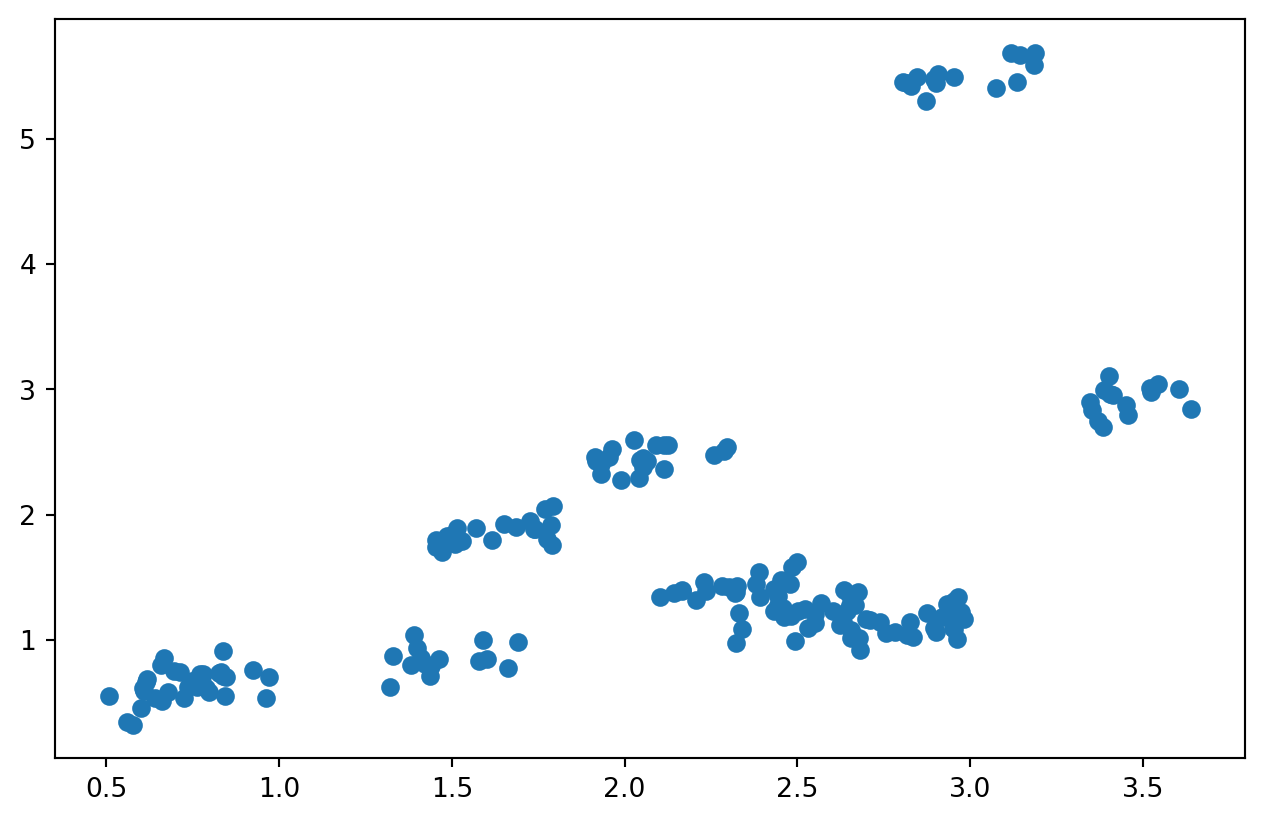

Med navn på dyrene

# Lage scatter-plot fordelt på dyr 
plt.figure(figsize=(8, 5))
for animal in animal_data['Animal'].unique():
    subset = animal_data[animal_data['Animal'] == animal]
    plt.scatter(subset['Length'], subset['Height'], label=animal)

# Pynt
plt.title('Animal Length vs Height')
plt.xlabel('Length (m)')
plt.ylabel('Height (m)')
plt.legend(title='Animal')
plt.show()

Envariabel lineær regresjon

from sklearn.linear_model import LinearRegression

# Prepare the data for linear regression
X = animal_data[['Length']]
y = animal_data['Height']

# Create and fit the model
model = LinearRegression()
model.fit(X, y)

# Predict the heights using the model
predicted_heights = model.predict(X)

# Plot the original data and the linear regression model
plt.figure(figsize=(8, 5))
plt.scatter(animal_data['Length'], animal_data['Height'], label='Actual Data')
plt.plot(animal_data['Length'], predicted_heights, color='red', label='Linear Regression Model')

# Add labels and title
plt.title('Linear Regression: Animal Length vs Height')
plt.xlabel('Length (m)')
plt.ylabel('Height (m)')
plt.legend()
plt.show()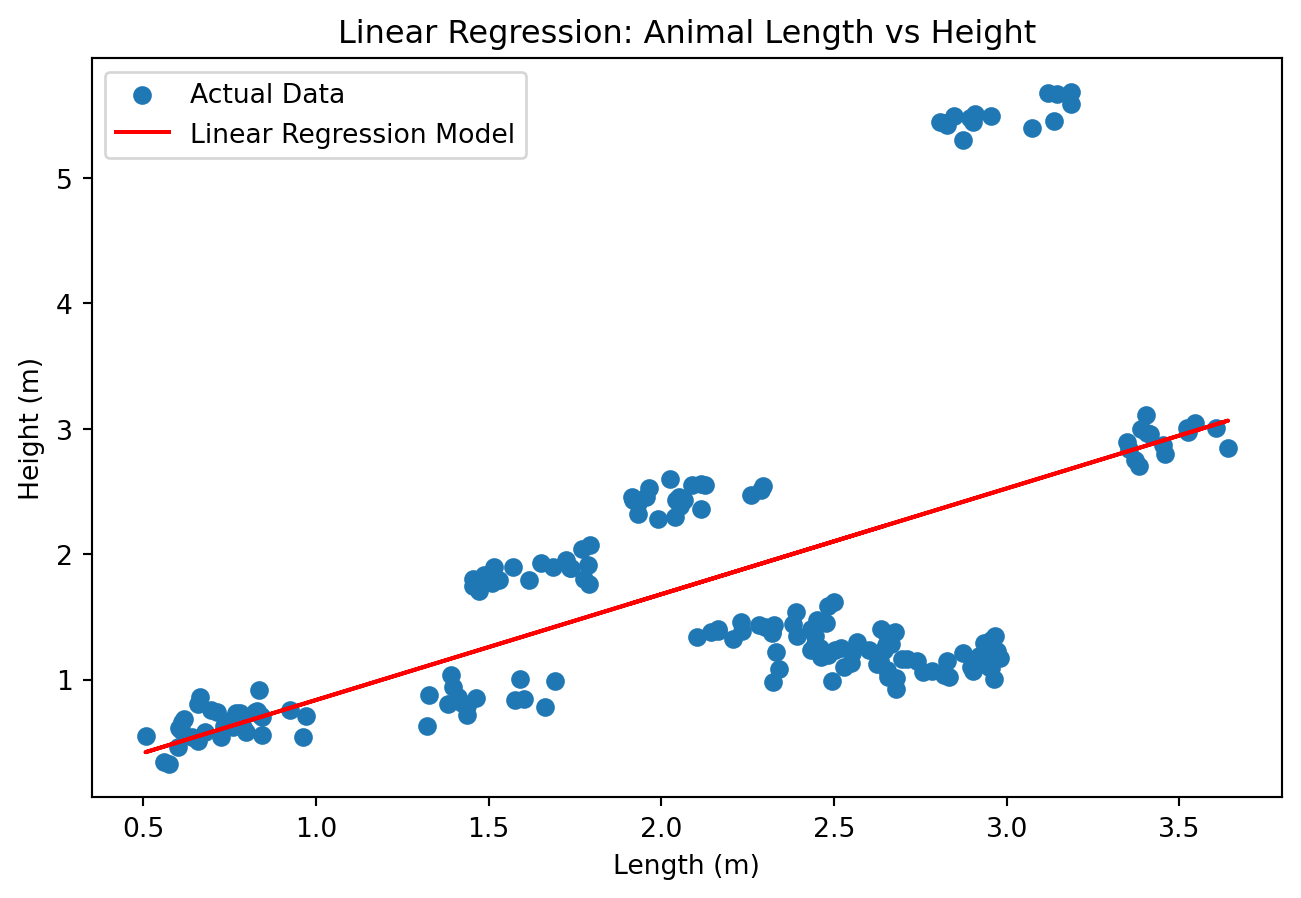

\[H(L, N) = \beta_0 + \beta_1 L\]

H	Høyde
L	Lengde
\(\beta_i\)	Regresjonskoeffisienter

Hvordan gjøre det bedre?

• forslag?

Hva med å numerisk kode dyrene?

from sklearn.linear_model import LinearRegression

# Encode the animal names as numbers
animal_data['Animal_Code'] = animal_data['Animal'].astype('category').cat.codes
# Display a random selection of 5 rows from the dataset
display(animal_data.sample(10))

	Animal	Length	Height	Animal_Code
40	Tiger	2.949765	1.097031	8
147	Koala	0.659256	0.801045	3
127	Panda	1.438418	0.790432	6
108	Kangaroo	1.500805	1.836083	2
152	Penguin	0.507209	0.551672	7
157	Penguin	0.778098	0.645235	7
171	Ostrich	2.051805	2.451676	5
174	Ostrich	1.964196	2.526428	5
43	Tiger	2.739377	1.144657	8
122	Panda	1.321700	0.626105	6

Illustrasjon av datasettet med tallkoder

# Plot the animal data with animal codes
plt.figure(figsize=(10, 6))
colors = plt.cm.get_cmap('tab10', len(animal_data['Animal'].unique()))

for i, animal in enumerate(animal_data['Animal'].unique()):
    subset = animal_data[animal_data['Animal'] == animal]
    plt.scatter(subset['Length'], subset['Height'], label=animal, color=colors(i))
    
    # Print the animal code above the average length and height
    avg_length = subset['Length'].mean()
    avg_height = subset['Height'].mean()
    plt.text(avg_length, avg_height + 0.3, f'{i}', fontsize=20, color=colors(i))

# Add labels and title
plt.title('Animal Length vs Height with Animal Codes')
plt.xlabel('Length (m)')
plt.ylabel('Height (m)')
plt.legend(title='Animal')
plt.show()

/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_10268/1848883834.py:3: MatplotlibDeprecationWarning:

The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.

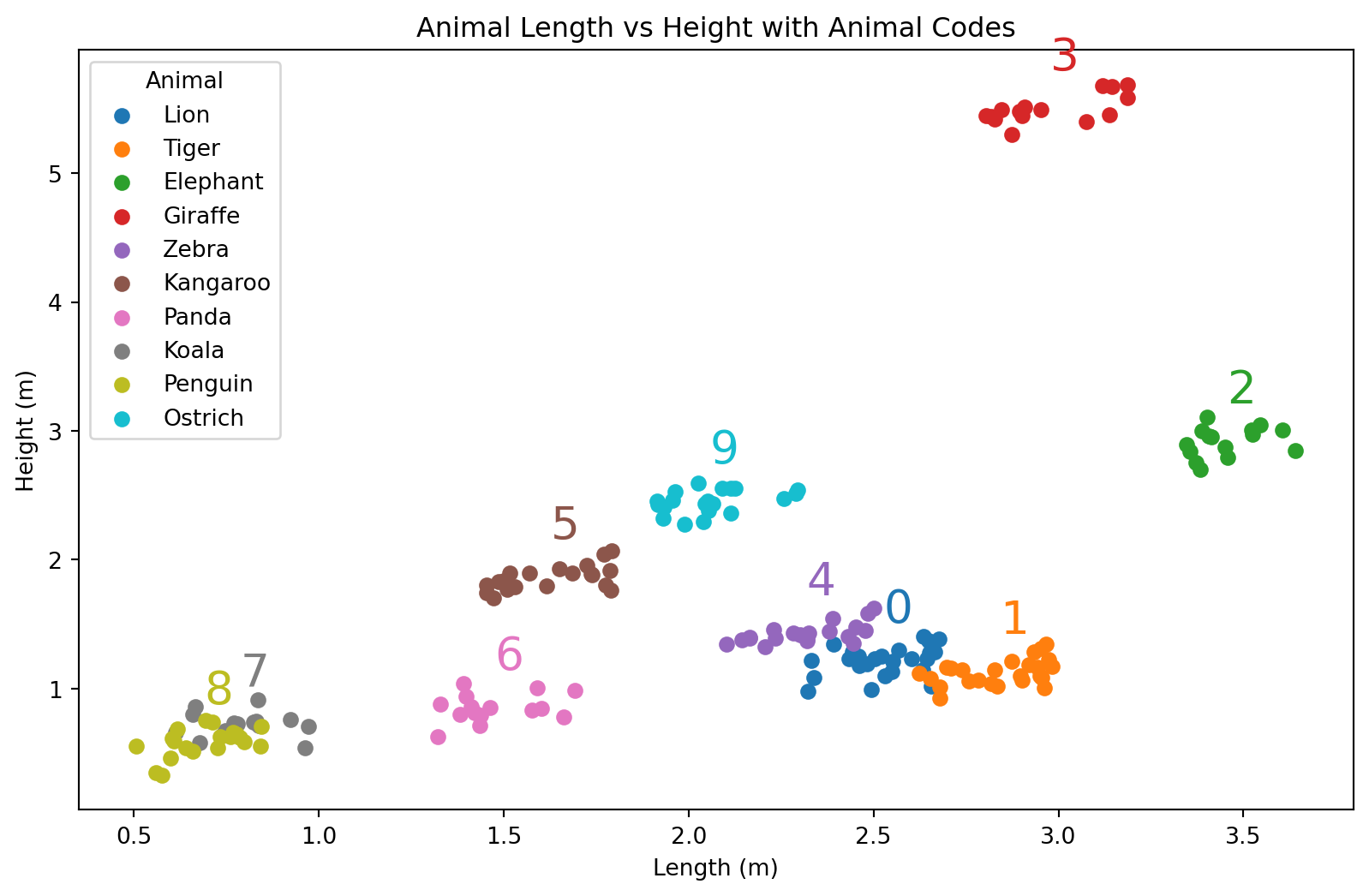
Lineær regresjon med tallkoder

# Prepare the data for linear regression
X = animal_data[['Length', 'Animal_Code']]
y = animal_data['Height']

# Create and fit the model
model = LinearRegression()
model.fit(X, y)

# Predict the heights using the model
predicted_heights = model.predict(X)

# Plot the original data and the linear regression model
plt.figure(figsize=(10, 6))
colors = plt.cm.get_cmap('tab10', len(animal_data['Animal'].unique()))

for i, animal in enumerate(animal_data['Animal'].unique()):
    subset = animal_data[animal_data['Animal'] == animal]
    plt.scatter(subset['Length'], subset['Height'], label=animal, color=colors(i))
    
    # Predict heights for the subset
    subset_X = subset[['Length', 'Animal_Code']]
    subset_predicted_heights = model.predict(subset_X)
    
    # Plot the regression line for the subset
    plt.plot(subset['Length'], subset_predicted_heights, color=colors(i))

    # Print the animal code above the average length and height
    avg_length = subset['Length'].mean()
    avg_height = subset['Height'].mean()
    plt.text(avg_length, avg_height + 0.3, f'{i}', fontsize=20, color=colors(i))

# Add labels and title
plt.title('Two Variable Linear Regression: Animal Length vs Height')
plt.xlabel('Length (m)')
plt.ylabel('Height (m)')
plt.legend(title='Animal')
plt.show()

/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_10268/389375858.py:14: MatplotlibDeprecationWarning:

The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.

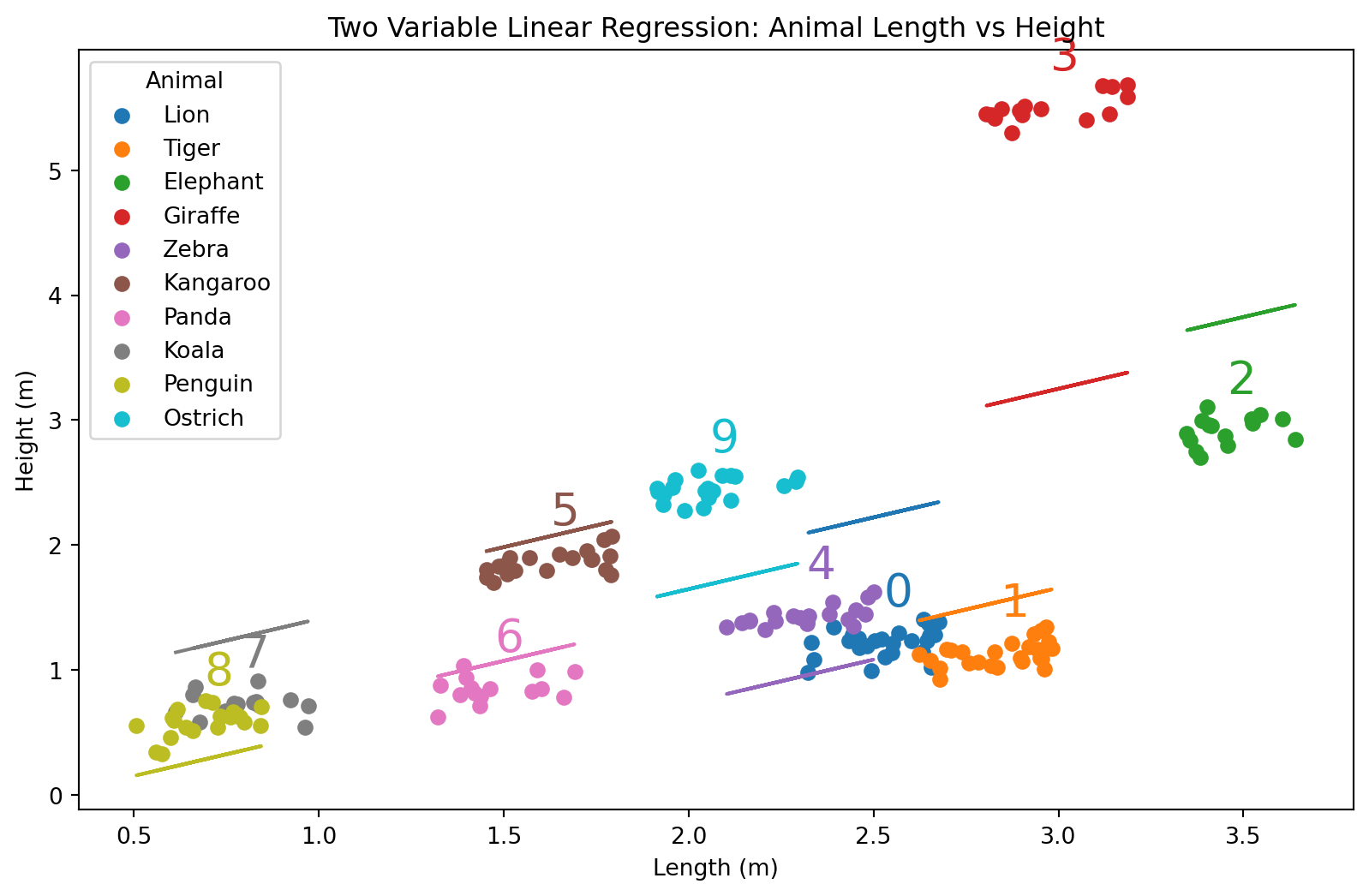
• Hvordan gikk egentlig dette? Se nøye etter.

Om vi ser på tallene, så ser vi at alle regresjonslinjene er sortert ettet tall. Det har altså noe å si hvordan dyrene er sortert. Bet blir litt rart.

Ligning

\[H(L, N) = \beta_0 + \beta_1 L + \beta_2 N\]

Symbol	Beskrivelse
H	Høyde
L	Lengde
N	Numerisk kode for dyret
\(\beta_i\)	Regresjonskoeffisienter

Hvordan gjøre det bedre?

• One-hot-encoding

Med one-hot encoding

Vi kan lage one-hot-kodet data med pandas.get_dummies(...)

from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer

transformed_data = pd.get_dummies(animal_data, columns=['Animal'], drop_first=False)
display(transformed_data.sample(10))

	Length	Height	Animal_Code	Animal_Elephant	Animal_Giraffe	Animal_Kangaroo	Animal_Koala	Animal_Lion	Animal_Ostrich	Animal_Panda	Animal_Penguin	Animal_Tiger	Animal_Zebra
19	2.666154	1.282923	4	0	0	0	0	1	0	0	0	0	0
169	0.787750	0.620942	7	0	0	0	0	0	0	0	1	0	0
39	2.623555	1.121049	8	0	0	0	0	0	0	0	0	1	0
133	1.436339	0.714177	6	0	0	0	0	0	0	1	0	0	0
78	3.074540	5.400244	1	0	1	0	0	0	0	0	0	0	0
175	2.289047	2.511948	5	0	0	0	0	0	1	0	0	0	0
29	2.901872	1.066009	8	0	0	0	0	0	0	0	0	1	0
106	1.724647	1.953400	2	0	0	1	0	0	0	0	0	0	0
117	1.616279	1.795778	2	0	0	1	0	0	0	0	0	0	0
176	1.932531	2.407404	5	0	0	0	0	0	1	0	0	0	0

Regresjonsmodell med one-hot-coding

X = transformed_data.drop(columns=['Height', 'Animal_Code'])
y = transformed_data['Height']

model = LinearRegression()
model.fit(X, y)

# Bruke modellen
predicted_heights = model.predict(X)

# Plot de originale dataene og den lineære regresjonsmodellen
plt.figure(figsize=(8, 5))
colors = plt.cm.get_cmap('tab10', len(animal_data['Animal'].unique()))

for i, animal in enumerate(animal_data['Animal'].unique()):
    subset = animal_data[animal_data['Animal'] == animal]
    plt.scatter(subset['Length'], subset['Height'], label=animal, color=colors(i), edgecolor=colors(i), facecolors='none')
    
    # Prediker høyder for hvert dyr 
    subset_X = transformed_data[transformed_data[f'Animal_{animal}'] == 1].drop(columns=['Height', 'Animal_Code'])
    subset_predicted_heights = model.predict(subset_X)
    
    # Plot regresjonslinjen for hvert enkelt dyr
    plt.plot(subset['Length'], subset_predicted_heights, color=np.array(colors(i))*0.9, linewidth=5)

# Pynt 
plt.title('Lineær regresjon med One-Hot Encoding: Dyrelengde vs Høyde')
plt.xlabel('Lengde (m)')
plt.ylabel('Høyde (m)')
plt.legend(title='Dyr')
plt.show()

/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_10268/1362502205.py:12: MatplotlibDeprecationWarning:

The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.

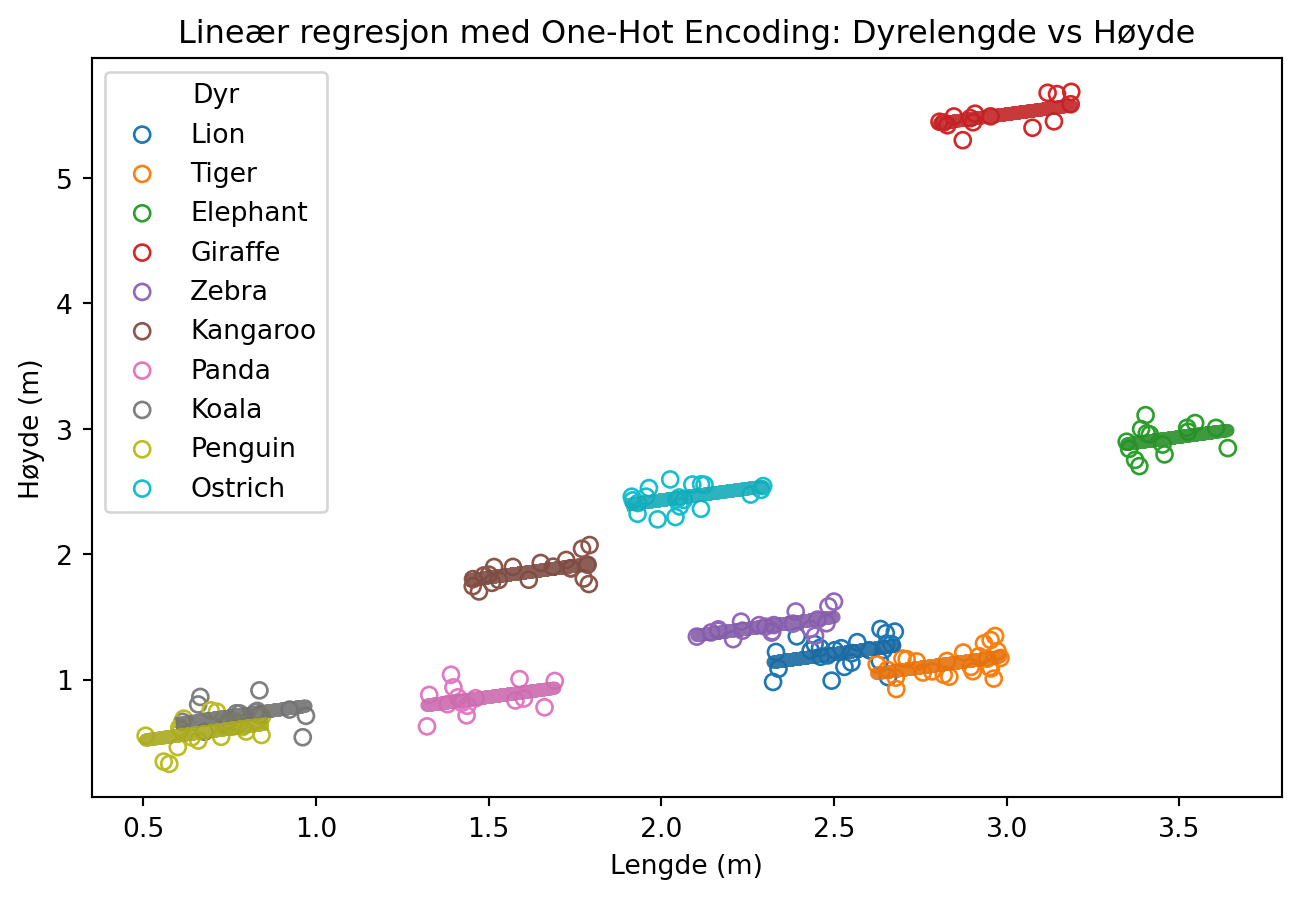
Likning

\[H(L, N) = \beta_0 + \beta_1 L + \sum_{\mathrm{i = \{Lion, Tiger, ...\}}}^{k} \beta_i [\text{er dette en }i\mathrm{?}]\]

La oss se på dette i et litt mindre datasett

import pandas as pd
import seaborn as sns
health = sns.load_dataset('healthexp')
display(health.sample(10))

	Year	Country	Spending_USD	Life_Expectancy
126	1996	France	2169.451	78.2
222	2012	France	4299.434	82.1
40	1980	Great Britain	385.099	73.2
154	2001	Canada	2624.293	79.3
272	2020	Japan	4665.641	84.7
84	1989	Canada	1579.543	77.1
250	2017	Canada	5150.470	81.9
201	2008	USA	7385.026	78.1
48	1982	Canada	996.086	75.6
110	1993	Japan	1332.213	79.4

Her bruker vi seaborn kun for å laste inn et datasett. Seaborn gir oss også noen muligheter til pen visualisering i statistikk, for dem som måtte være interessert i det.

Underveisoppgave

Note

1. Gjør one-hot encoding av healthexp-datasettet
2. Gjør trenings-validerings-splitt av datasettet
3. Tren en lineær regresjonsmodell for å predikere life expectancy, med spending som forklaringsvariabel
4. Ta med land som forklaringsvariabel i modellen
5. Sammenligne nøyaktigehten til modellene

import pandas as pd
import seaborn as sns
health = sns.load_dataset('healthexp')
health_onehot = pd.get_dummies(health, columns=['Country'])
display(health_onehot.sample(10))

	Year	Spending_USD	Life_Expectancy	Country_Canada	Country_France	Country_Germany	Country_Great Britain	Country_Japan	Country_USA
223	2012	3614.131	81.0	0	0	0	1	0	0
171	2003	5726.538	77.1	0	0	0	0	0	1
211	2010	3441.710	80.6	0	0	0	1	0	0
93	1990	1088.959	78.9	0	0	0	0	1	0
131	1997	2496.201	77.3	0	0	1	0	0	0
249	2016	9717.649	78.7	0	0	0	0	0	1
193	2007	3021.671	79.7	0	0	0	1	0	0
209	2010	4423.070	80.5	0	0	1	0	0	0
149	2000	2895.533	78.2	0	0	1	0	0	0
163	2002	2287.476	78.3	0	0	0	1	0	0

for i, frame in health.groupby("Country"):
    plt.scatter(frame["Spending_USD"], frame["Life_Expectancy"], marker="o", label=i)
plt.xlabel("Expenditure (USD)")
plt.ylabel("Life expectancy")
plt.legend()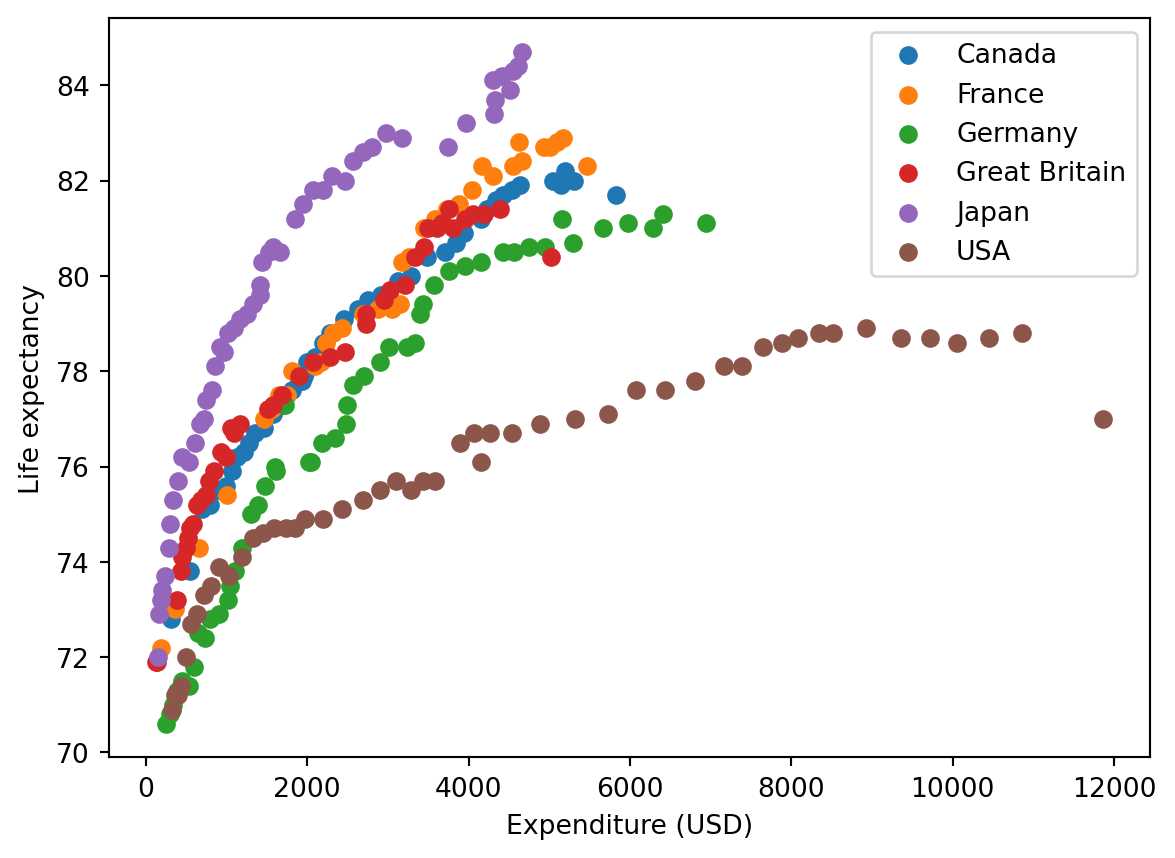

Start på løsning

health_onehot = pd.get_dummies(health, columns=['Country'], drop_first=False)
display(health.sample(10))

	Year	Country	Spending_USD	Life_Expectancy
74	1987	Canada	1357.453	76.7
57	1983	USA	1451.945	74.6
159	2001	USA	4888.518	76.9
153	2000	USA	4536.561	76.7
152	2000	Japan	1847.786	81.2
52	1982	USA	1329.669	74.5
137	1998	Germany	2566.003	77.7
22	1975	USA	560.750	72.7
113	1994	Germany	2188.676	76.5
104	1992	Japan	1253.415	79.2

Enkel regresjonsmodell

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

X = np.array(health_onehot["Spending_USD"]).reshape(-1,1)
y = health_onehot['Life_Expectancy']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create and fit the model on the training data
model = LinearRegression()
model.fit(X_train, y_train)

# Predict the life expectancy using the model on the test data
predicted_life_expectancy = model.predict(X_test)

# Evaluate the model
from sklearn.metrics import mean_squared_error, r2_score

mse = mean_squared_error(y_test, predicted_life_expectancy)
r2 = r2_score(y_test, predicted_life_expectancy)

# Plot the original data and the linear regression model
plt.figure(figsize=(8, 5))
plt.scatter(X_test, y_test, color='blue', label='Actual Data')
plt.plot(X_test, predicted_life_expectancy, color='red', label='Linear Regression Model')

# Add labels and title
plt.title('Linear Regression: Spending vs Life Expectancy')
plt.xlabel('Spending (USD)')
plt.ylabel('Life Expectancy (years)')
plt.legend()
plt.show()
print(f'Mean Squared Error: {mse}')
print(f'R^2 Score: {r2}')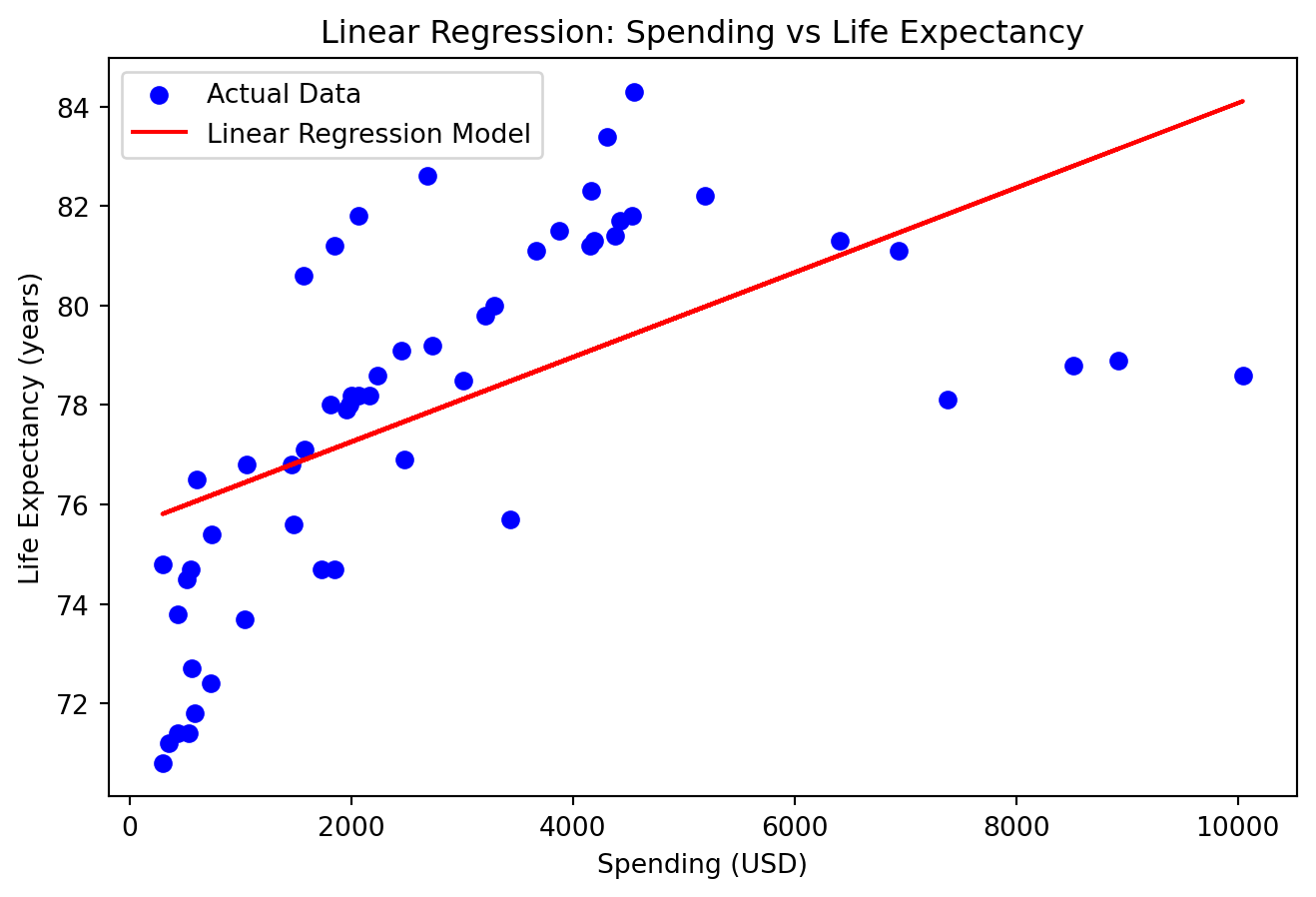

Mean Squared Error: 7.846016617615249
R^2 Score: 0.3573359515082699

En påfallende “god” modell, hva har skjedd her?

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split

X = health_onehot.drop(columns=['Life_Expectancy'])
y = health_onehot['Life_Expectancy']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create and fit the model on the training data
model = LinearRegression()
model.fit(X_train, y_train)

# Predict the life expectancy using the model on the test data
predicted_life_expectancy = model.predict(X_test)

# Evaluate the model
mse = mean_squared_error(y_test, predicted_life_expectancy)
r2 = r2_score(y_test, predicted_life_expectancy)


# Plot the original data and the linear regression model predictions per country
plt.figure(figsize=(8, 5))
colors = plt.cm.get_cmap('tab20', len(health['Country'].unique()))

for i, country in enumerate(health['Country'].unique()):
    subset = health[health['Country'] == country]
    plt.scatter(subset['Spending_USD'], subset['Life_Expectancy'], label=country, color=colors(i), edgecolor=colors(i), facecolors='none')
    
    # Predict life expectancy for the subset
    subset_X = health_onehot[health_onehot[f'Country_{country}'] == 1].drop(columns=['Life_Expectancy'])
    subset_predicted_life_expectancy = model.predict(subset_X)
    
    # Plot the regression line for the subset
    plt.plot(subset['Spending_USD'], subset_predicted_life_expectancy, color=np.array(colors(i))*0.9, linewidth=2)

# Add labels and title
plt.title('Linear Regression with One-Hot Encoding: Spending vs Life Expectancy by Country')
plt.xlabel('Spending (USD)')
plt.ylabel('Life Expectancy (years)')
plt.legend(title='Country', bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()
print(f'Mean Squared Error: {mse}')
print(f'R^2 Score: {r2}')

/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_10268/1590429931.py:24: MatplotlibDeprecationWarning:

The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.

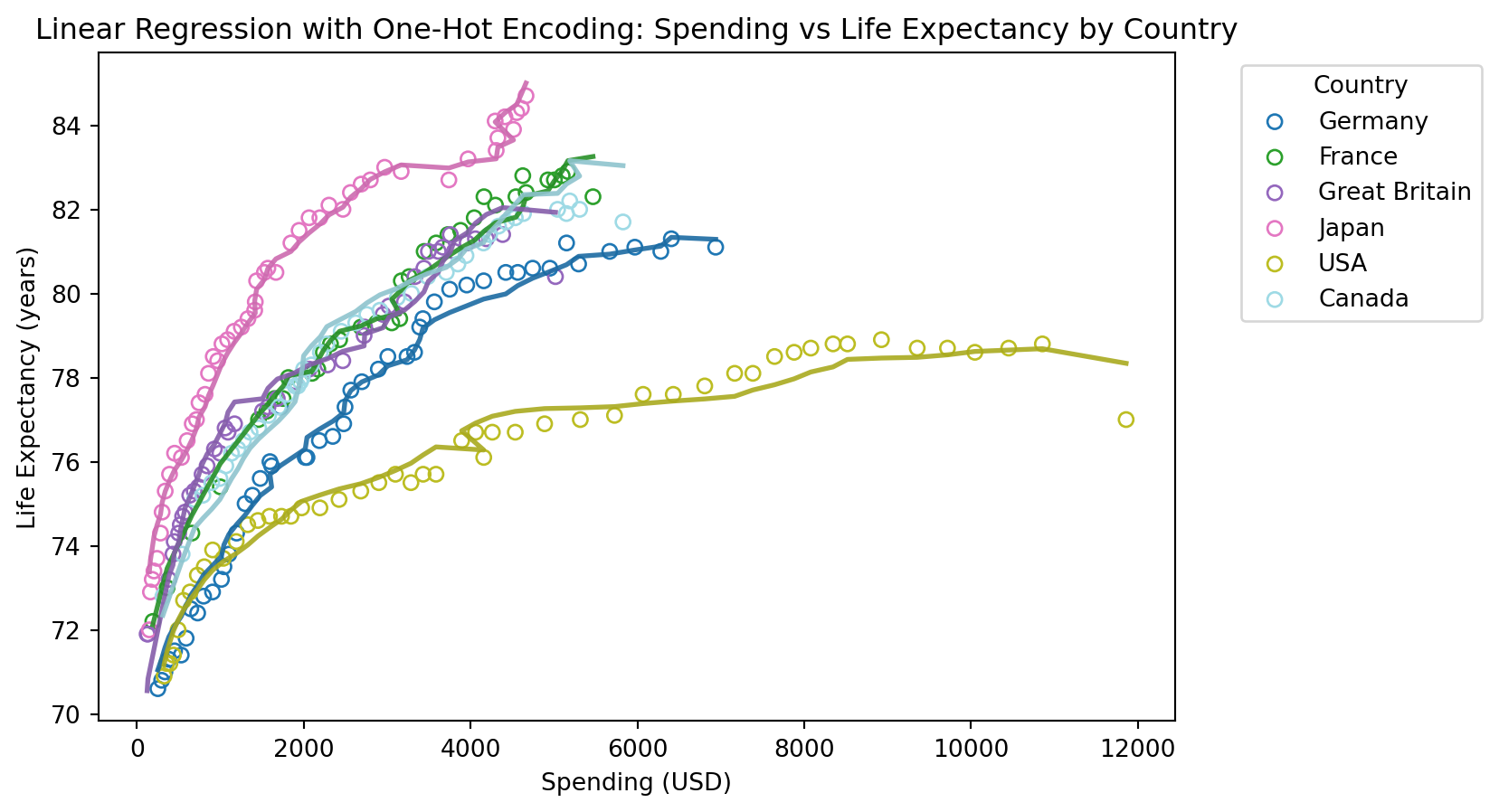
Mean Squared Error: 0.13772868450150377
R^2 Score: 0.9887186991451874

Uten år som forklaringsvariabel

# Drop the 'Year' column from the dataset
health_onehot_no_year = health_onehot.drop(columns=['Year'])

# Prepare the data for linear regression
X = health_onehot_no_year.drop(columns=['Life_Expectancy'])
y = health_onehot_no_year['Life_Expectancy']

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create and fit the model on the training data
model = LinearRegression()
model.fit(X_train, y_train)

# Predict the life expectancy using the model on the test data
predicted_life_expectancy = model.predict(X_test)

# Evaluate the model
mse = mean_squared_error(y_test, predicted_life_expectancy)
r2 = r2_score(y_test, predicted_life_expectancy)

# Plot the original data and the linear regression model predictions per country
plt.figure(figsize=(8, 5))
colors = plt.cm.get_cmap('tab20', len(health['Country'].unique()))

for i, country in enumerate(health['Country'].unique()):
    subset = health[health['Country'] == country]
    plt.scatter(subset['Spending_USD'], subset['Life_Expectancy'], label=country, color=colors(i), edgecolor=colors(i), facecolors='none')
    
    # Predict life expectancy for the subset
    subset_X = health_onehot_no_year[health_onehot_no_year[f'Country_{country}'] == 1].drop(columns=['Life_Expectancy'])
    subset_predicted_life_expectancy = model.predict(subset_X)
    
    # Plot the regression line for the subset
    plt.plot(subset['Spending_USD'], subset_predicted_life_expectancy, color=np.array(colors(i))*0.9, linewidth=2)

# Add labels and title
plt.title('Linear Regression with One-Hot Encoding (No Year): Spending vs Life Expectancy by Country')
plt.xlabel('Spending (USD)')
plt.ylabel('Life Expectancy (years)')
plt.legend(title='Country', bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()
print(f'Mean Squared Error: {mse}')
print(f'R^2 Score: {r2}')

/var/folders/qn/3_cqp_vx25v4w6yrx68654q80000gp/T/ipykernel_10268/3728857717.py:24: MatplotlibDeprecationWarning:

The get_cmap function was deprecated in Matplotlib 3.7 and will be removed two minor releases later. Use ``matplotlib.colormaps[name]`` or ``matplotlib.colormaps.get_cmap(obj)`` instead.

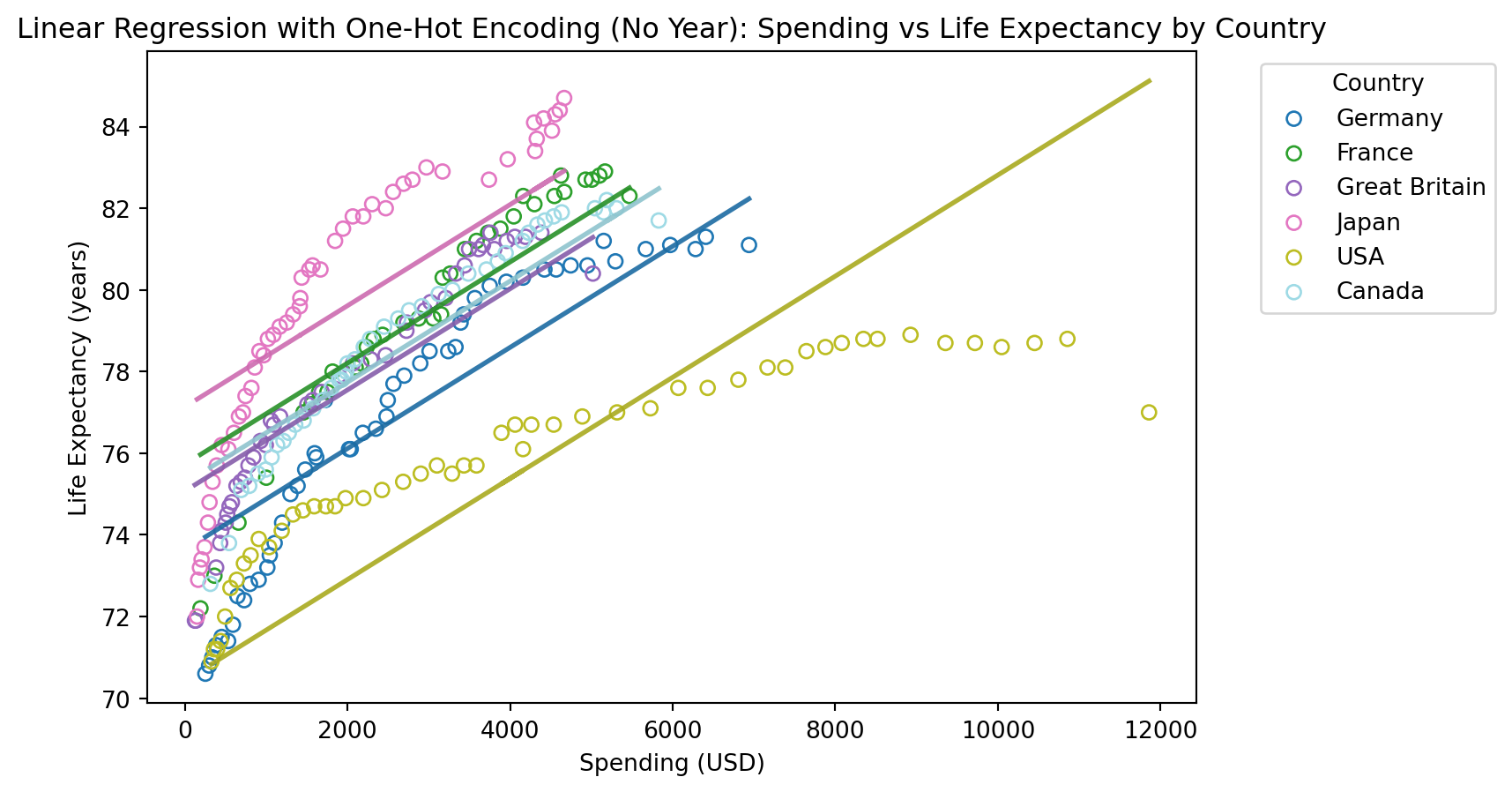
Mean Squared Error: 2.3013732097838697
R^2 Score: 0.8114954509821513