import pandas as pd
df = pd.read_csv("./data/apple_quality.csv")Forelesningsnotat: Ensemblemetoder
Slides
En samling av beslutningstrær
- Beslutningstrær alene har noen svakheter:
- Ikke topp nøyaktighet
- Ikke robuste
Hva kan vi gjøre med det?
Ensemble-metoder
- bagging
- Random Forest
Vi skal nå bygge oss opp dit vha eple-oppgaven.
Beslutningstre: eplekvalitet
(Kode-eksempel)
Vi skal bruke beslutningstrær på et datasett som inneholder informasjon om 4000 epler (størrelse, vekt, saftighet, søthet, syrlighet etc.) og lage en modell som kan si om eplet er av god eller dårlig kvalitet.
Først må vi laste inn datasettet som en csv-fil. Dere kan laste det ned her her og lese det rett inn slik
Vi ønsker å lage et beslutningstre som basert på alle parameterne kan si noe om kvaliteten på eplet.
- Undersøk datasettet. Inneholder det NaN eller ugyldige verdier? Fjern disse i såfall.
# Vi sjekker hvor my nan det er, slik at vi får verifisert at vi ikke sletter en hel masse
print(df.isnull().sum())
# Remove rows with NaN values
df = df.dropna()
# Verify that NaN values are removed
print(df.isnull().sum())A_id 1
Size 1
Weight 1
Sweetness 1
Crunchiness 1
Juiciness 1
Ripeness 1
Acidity 0
Quality 1
dtype: int64
A_id 0
Size 0
Weight 0
Sweetness 0
Crunchiness 0
Juiciness 0
Ripeness 0
Acidity 0
Quality 0
dtype: int64- Hvilke kategorier har vi for kvaliteten på eplene (Quality)?
print(df['Quality'].unique())['good' 'bad']Kvalitetene er “good” og “bad”.
- Definer prediktorene og responsen/target til modellen og definer nødvendige numpy-arrays. Er det noen kolonner som ikke bør tas med i modellen? Du bør også gjøre om definisjonen av kvalitet i respons-vektoren din til tall. F.eks. vha. lambda-funksjoner
df['quality_num'] = df['Quality'].apply(lambda x: 1.0 if x == "good" else 0.0)
df| A_id | Size | Weight | Sweetness | Crunchiness | Juiciness | Ripeness | Acidity | Quality | quality_num | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -3.970049 | -2.512336 | 5.346330 | -1.012009 | 1.844900 | 0.329840 | -0.491590483 | good | 1.0 |
| 1 | 1.0 | -1.195217 | -2.839257 | 3.664059 | 1.588232 | 0.853286 | 0.867530 | -0.722809367 | good | 1.0 |
| 2 | 2.0 | -0.292024 | -1.351282 | -1.738429 | -0.342616 | 2.838636 | -0.038033 | 2.621636473 | bad | 0.0 |
| 3 | 3.0 | -0.657196 | -2.271627 | 1.324874 | -0.097875 | 3.637970 | -3.413761 | 0.790723217 | good | 1.0 |
| 4 | 4.0 | 1.364217 | -1.296612 | -0.384658 | -0.553006 | 3.030874 | -1.303849 | 0.501984036 | good | 1.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 3995 | 3995.0 | 0.059386 | -1.067408 | -3.714549 | 0.473052 | 1.697986 | 2.244055 | 0.137784369 | bad | 0.0 |
| 3996 | 3996.0 | -0.293118 | 1.949253 | -0.204020 | -0.640196 | 0.024523 | -1.087900 | 1.854235285 | good | 1.0 |
| 3997 | 3997.0 | -2.634515 | -2.138247 | -2.440461 | 0.657223 | 2.199709 | 4.763859 | -1.334611391 | bad | 0.0 |
| 3998 | 3998.0 | -4.008004 | -1.779337 | 2.366397 | -0.200329 | 2.161435 | 0.214488 | -2.229719806 | good | 1.0 |
| 3999 | 3999.0 | 0.278540 | -1.715505 | 0.121217 | -1.154075 | 1.266677 | -0.776571 | 1.599796456 | good | 1.0 |
4000 rows × 10 columns
- Lag et beslutningtre og vurder hvor god modellen er til å predikere kvaliteten på eplene.
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# Split the data into training and testing sets
X = df.drop(columns=['Quality', 'quality_num'])
y = df['quality_num']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)
clf = DecisionTreeClassifier(random_state=10)
clf.fit(X_train, y_train)
# Make predictions on the test set
y_pred = clf.predict(X_test)
# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
import matplotlib.pyplot as plt
from sklearn import tree
# Visualize the decision tree
plt.figure(figsize=(20,10))
tree.plot_tree(clf, feature_names=X.columns, class_names=['bad', 'good'], filled=True)
plt.show()La oss så se hva som skjer om vi kjører mange ganger, fordelingen av nøyaktighet blir da?
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# Split the data into training and testing sets
X = df.drop(columns=['Quality', 'quality_num'])
y = df['quality_num']
accuracies = []
for random_state in range(10):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=random_state)
clf = DecisionTreeClassifier(random_state=random_state)
clf.fit(X_train, y_train)
# Make predictions on the test set
y_pred = clf.predict(X_test)
# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
accuracies.append(accuracy)
import matplotlib.pyplot as plt
plt.hist(accuracies)
from sklearn import tree
# Visualize the decision tree
plt.figure(figsize=(20,10))
tree.plot_tree(clf, feature_names=X.columns, class_names=['bad', 'good'], filled=True)
plt.show()Her hopper vi av og fortsetter med bagging i stedet. Hva skjer om vi lager mange trær med forskjellig random state, og bruker gjennomsnittet av prediksjonene til å bestemme oss for om eplet er bra eller dårlig? Majority vote.
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import numpy as np
# Split the data into training and testing sets
X = df.drop(columns=['Quality', 'quality_num'])
y = df['quality_num']
accuracies = []
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)
y_preds = np.zeros(len(y_test))
N_trees_in_bag = 10
for random_state in range(N_trees_in_bag):
X_bag, _, y_bag, _ = train_test_split(X_train, y_train, test_size=0.1, random_state=random_state)
clf = DecisionTreeClassifier(random_state=random_state)
clf.fit(X_bag, y_bag)
# Make predictions on the test set
y_preds += clf.predict(X_test)
bag_pred = np.round(y_preds/N_trees_in_bag)
accuracy = accuracy_score(y_test, bag_pred)
print(f"Accuracy: {accuracy:.2f}")Accuracy: 0.83Konklusjon fra bagging
Vi får bedre nøyaktighet. Andre ting?
Random forest
Så skal vi prøve med random forest.
- Mer uavhengige trær enn bare en haug med trær
(Hvordan uavhengige? ->)
Hvordan lages vanlige beslutningstrær
Først: For hele datasettet, finn den prediktoren, og den verdien for den prediktoren som gir best prediksjon når den brukes til å dele datasettet i to.
Deretter, så mange ganger som nødvendig: For hver av bladnodene, så lenge det er mulig å forbedre prediksjonen, gjenta punktet over
Hvordan lages beslutningstrær i en random forest?
- I stedet for å velge den prediktoren som best deler datasettet, så velger man ved hver mulighet en tilfeldig prediktor blant en undergruppe av prediktorene.
Alle: ['A_id', 'Size', 'Weight', 'Sweetness', 'Crunchiness', 'Juiciness', 'Ripeness', 'Acidity']
Tilfeldig undergruppe: ['A_id', 'Size', 'Sweetness', 'Crunchiness']
Tilfeldig undergruppe: ['Weight', 'Sweetness', 'Crunchiness', 'Acidity']
Tilfeldig undergruppe: ['A_id', 'Weight', 'Crunchiness', 'Acidity']
Tilfeldig undergruppe: ['A_id', 'Weight', 'Juiciness', 'Acidity']
Tilfeldig undergruppe: ['Weight', 'Sweetness', 'Juiciness', 'Ripeness']- Ikke alle trærne blir “optimale”, men når de får virke sammen, gir mangfoldet en fordel!
La oss prøve med en random forest
(Kode-eksempel)
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
import pandas as pd
df = pd.read_csv("./data/apple_quality.csv")
df = df.dropna()
# Split the data into training and testing sets
X = df.drop(columns=['Quality'])
y = df['Quality']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create a random forest classifier
rf_clf = RandomForestClassifier(n_estimators=20, random_state=42)
# Train the classifier
rf_clf.fit(X_train, y_train)
# Make predictions on the test set
y_pred = rf_clf.predict(X_test)
# Evaluate the model
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")Accuracy: 0.88Hva har vi mistet?
Da vi begynte med trær, sa vi at de er bra fordi de er så enkle å tolke. Hva nå?
- Vi trenger nye måter å karakterisere modellene våre på
Partial dependence
Hva er det?
- Bruker modellen på alle datapunktene i treningsdataene (og eller testdataene).
- Ser så på effekten av variere på én av prediktorene ad gangen.
Partial dependence
(Kode-eksempel)
from sklearn.inspection import PartialDependenceDisplay
import matplotlib.pyplot as plt
import numpy as np
# Plot partial dependence
features = X.select_dtypes(include=[np.number]).columns.tolist()
fig, ax = plt.subplots(figsize=(8, 8))
plots = PartialDependenceDisplay.from_estimator(rf_clf, X_train, features, grid_resolution=20, ax=ax)
for ax in plots.axes_.ravel():
try:
ax.set_ylim(0, 1)
except AttributeError as e:
pass
fig.tight_layout()
plt.show()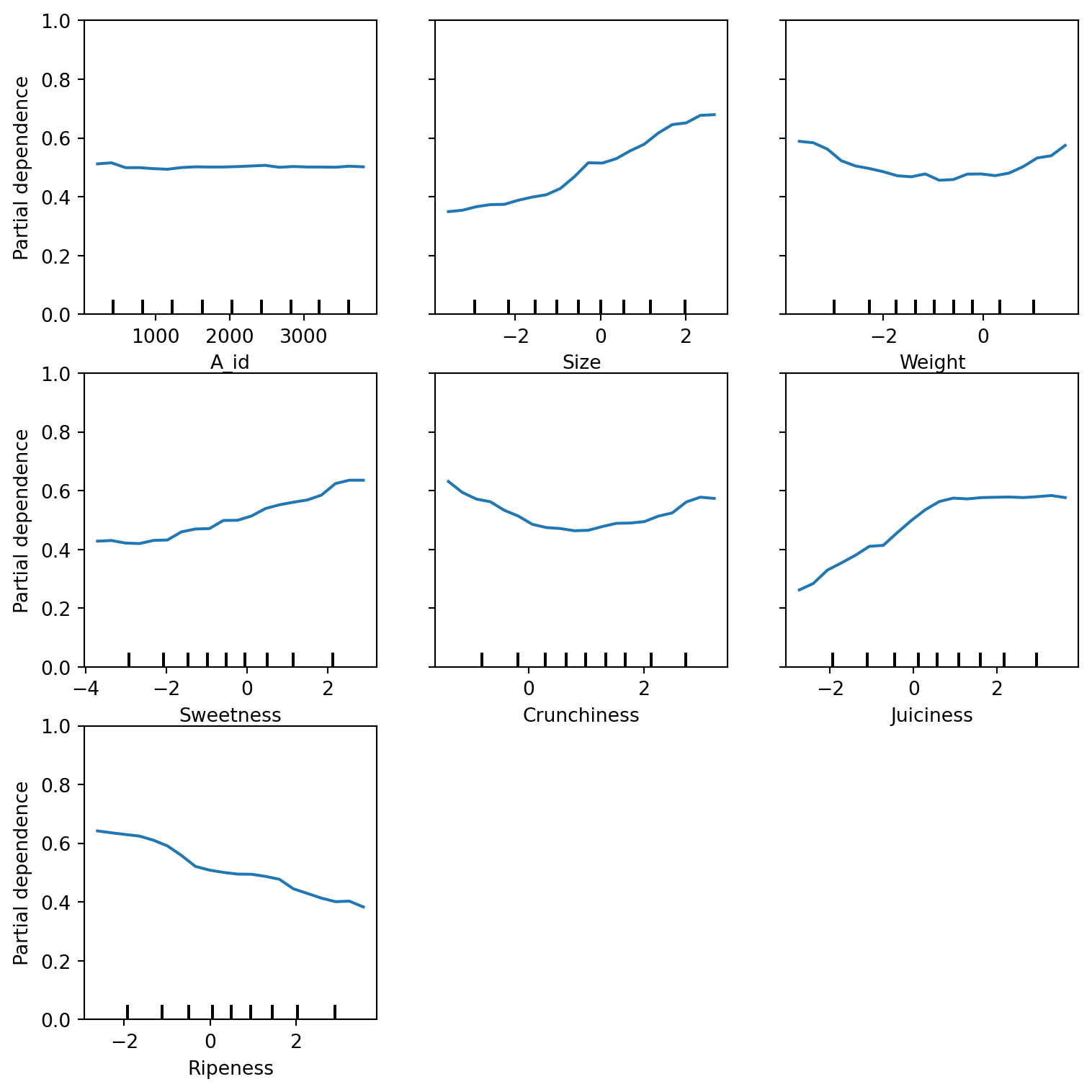
Hvis tid
Nå har vi sett på følgende måter å lage en tre-basert modell:
- Beslutningstre
- Haug med beslutningstrær
- Random forest
Beregn nøyaktigheten til eple-modellen som funksjon av antallet trær (weak learners) for haug med trær (bagging) og for random forest.
Hvis mer tid
- Starte på obligen
Til neste gang
- Starte på obligen–da får du mer ut av neste time